1. 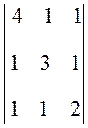 . Ответ:
17.
. Ответ:
17.
2. 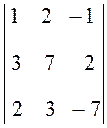 . Ответ: 0.
. Ответ: 0.
3. 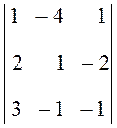 . Ответ:
8.
. Ответ:
8.
4. 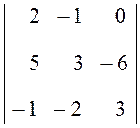 . Ответ:
3.
. Ответ:
3.
Определение
Если в матрице А заменить строки на столбцы, то полученная
матрица называется транспонированной и обозначается А![]() .
.
Пример
Пусть А = 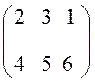 . Тогда А
. Тогда А![]() =
= 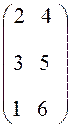 .
.
Свойство 1. При транспонировании матрицы величина определителя не меняется.
Проверим это на конкретном примере.
Пример
Пусть А = 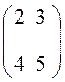 . Тогда А
. Тогда А![]() =
= 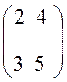 . DА =
2 × 5 - 3 ×
4 = -2,
. DА =
2 × 5 - 3 ×
4 = -2,
DА![]() = 5 ×
2 - 4 × 3 =
-2 = DА, что и
требовалось показать.
= 5 ×
2 - 4 × 3 =
-2 = DА, что и
требовалось показать.
Свойство 2. Если в определителе поменять местами две строки (два столбца), то определитель изменит знак на противоположный.
Пример
Пусть А = 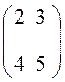 . Тогда А
. Тогда А![]() =
= 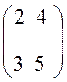 . DА =
2 × 5 - 3 × 4 =
-2,
. DА =
2 × 5 - 3 × 4 =
-2,
DА![]() = 5 ×
2 - 4
× 3 =
-2 = DА, что и
требовалось показать.
= 5 ×
2 - 4
× 3 =
-2 = DА, что и
требовалось показать.
Свойство 3. Если все элементы какой-нибудь строки (столбца) умножить на
l ¹ 0, то и весь определитель также умножится на l.
Свойство 3¢(следствие свойства 3). Множитель, общий для всех элементов строки (столбца), можно вынести за знак определителя
D = 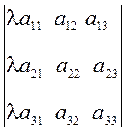 = l
= l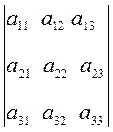 .
.
Пример
Вычислить определитель:
D = 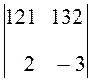 = 121(-3) - 2×132
= - 363 - 264 = -627.
С другой стороны, воспользовавшись свойством 3¢,
имеем
= 121(-3) - 2×132
= - 363 - 264 = -627.
С другой стороны, воспользовавшись свойством 3¢,
имеем
D = 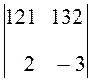 =
= 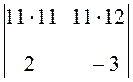 =
11
=
11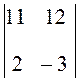 =
11(11(-3) - 2×12)
=
=
11(11(-3) - 2×12)
=
= 11(-33 - 24) = 11(-57) = -627.
Свойство 4. Если к элементам одной строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится
D = 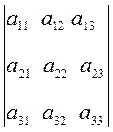 =
= 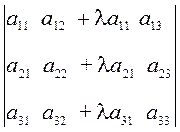 .
.
В приведенной иллюстрации к элементам второго столбца добавлены элементы первого столбца, умноженные на произвольное l. На практике произошло преобразование второго столбца. Подобные преобразования определителей можно записывать следующим образом:
а) первую, вторую, третью строки условно обозначим a![]() , a
, a![]() , a
, a![]() ;
;
б) первый, второй, третий столбцы обозначим как в![]() , в
, в![]() , в
, в![]() .
.
Тогда проведенное преобразование определителя в этих терминах
можно записать так: в![]() ® в
® в![]() + l в
+ l в![]() .
.
Упражнение 6
Вычислить определитель D
= 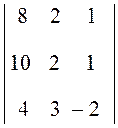 .
.
Решение
1. Вынесем общий множитель для всех элементов первого столбца за знак определителя
D = 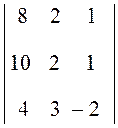 = 2
= 2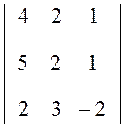 .
.
2. Вычтем из элементов второй строки элементы первой строки
(преобразование a![]() – a
– a![]() )
)
D = 2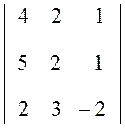 = 2
= 2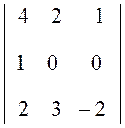 .
.
a![]() – a
– a![]()
3. Прибавим к элементам третьей строки элементы первой
строки, умножив их на 2 (преобразование a![]() + 2 a
+ 2 a![]() ),
),
D = 2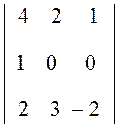 = 2
= 2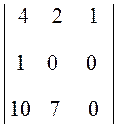 .
.
a![]() + 2 a
+ 2 a![]()
4. Воспользовавшись правилом Саррюса, вычислим последний определитель непосредственно
D = 2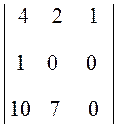 = 2((4×0×0 + 2×0×10 + 1×1×7) -
(10×0×1
+ 7×0×4
+ 0×1×2))
= 14.
= 2((4×0×0 + 2×0×10 + 1×1×7) -
(10×0×1
+ 7×0×4
+ 0×1×2))
= 14.
Замечание
Появление в результате проведенных преобразований элементов, равных нулю, в значительной степени упростило процесс непосредственных вычислений. Так, в приведенном примере из шести слагаемых не равным нулю оказалось только одно.
Свойства 3 и 4 являются одними из наиболе е употребительных при вычислении определителей. Следующее же свойство ввиду своей важности заслуживает отдельного рассмотрения.
Определение
В матрице A n-го порядка вычеркнем i-ю
строку и j-й столбец. Сдвинем оставшиеся элементы, не нарушая порядка.
Определитель полученной матрицы порядка (n - 1) называется минором элемента a![]() , находящегося на пересечении i-й
строки и j-го столбца, и обозначается D
, находящегося на пересечении i-й
строки и j-го столбца, и обозначается D![]() .
.
Пример
Найдем миноры D![]() и D
и D![]() определителя
определителя 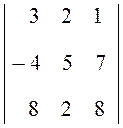 .
.
Элементы а![]() = 7,
а а
= 7,
а а![]() = 2.
= 2.
Вычеркнем вторую строку и третий столбец в исходном определителе,
в результате получим минор D![]() :D
:D![]() =
=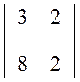 =6 – 16=-10.
=6 – 16=-10.
Вычеркнем третью строку и второй столбец в исходном определителе,
получим минор D![]() :
D
:
D![]() =
= 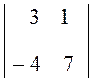 = 21 + 4 = 25.
= 21 + 4 = 25.
Пример
Найти все миноры для определителя второго порядка 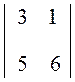 .
.
Легко увидеть, что в определителе второго порядка минорами являются сами элементы исходного определителя, которые получаются при вычеркивании соответствующих строк и столбцов
D![]() = 6, D
= 6, D![]() = 5, D
= 5, D![]() = 1, D
= 1, D![]() = 3.
= 3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.