Лабораторная работа
по информатике:
«Численные методы решения нелинейных уравнений»
Выполнил:
Гаврилин Дмитрий,
студент
421 группы
Цели работы:
1) Изучить методы нахождения корней нелинейного уравнения вида f(x)=0, где f(x)
- некоторая непрерывная функция.
Методы, использованные в данной лабораторной работе:
Excel:
-построение таблицы, графика и вывод результатов
Fortran:
-метод
половинного деления
-метод касательных
-zreal
2) Сравнить результаты данных методов
3) Выбрать наиболее точный метод
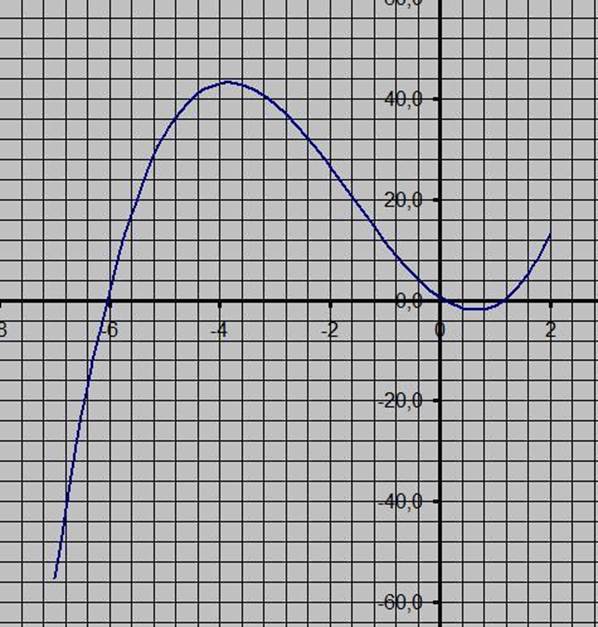
Excel: построение таблицы, графика и вывод результатов.
|
x |
y=f(x) |
|
-7 |
-55,2 |
|
-6,8 |
-41,4 |
|
-6,6 |
-28,8 |
|
-6,4 |
-17,4 |
|
-6,2 |
-7,2 |
|
-6 |
1,9 |
|
-5,8 |
10,0 |
|
-5,6 |
17,0 |
|
-5,4 |
23,1 |
|
-5,2 |
28,3 |
|
-5 |
32,7 |
|
-4,8 |
36,2 |
|
-4,6 |
38,9 |
|
-4,4 |
40,9 |
|
-4,2 |
42,3 |
|
-4 |
43,0 |
|
-3,8 |
43,1 |
|
-3,6 |
42,8 |
|
-3,4 |
41,9 |
|
-3,2 |
40,6 |
|
-3 |
39,0 |
|
-2,8 |
36,9 |
|
-2,6 |
34,7 |
|
-2,4 |
32,1 |
|
-2,2 |
29,4 |
|
-2 |
26,5 |
|
-1,8 |
23,6 |
|
-1,6 |
20,6 |
|
-1,4 |
17,6 |
|
-1,2 |
14,6 |
|
-1 |
11,7 |
|
-0,8 |
9,0 |
|
-0,6 |
6,5 |
|
-0,4 |
4,2 |
|
-0,2 |
2,2 |
|
0 |
0,6 |
|
0,2 |
-0,7 |
|
0,4 |
-1,6 |
|
0,6 |
-1,9 |
|
0,8 |
-1,8 |
|
1 |
-1,0 |
|
1,2 |
0,4 |
|
1,4 |
2,4 |
|
1,6 |
5,2 |
|
1,8 |
8,7 |
|
2 |
13,1 |
|
Корень |
Значение корня |
Значение функции |
|
1. |
-6,04437 |
-0,0000064 |
|
2. |
0,078739 |
0,0000032 |
|
3. |
1,155627 |
-0,0000311 |
Fortran: метод половинного деления.
Текст программы:
1.
program piw
real a,f,x,eps,b
external f
print *,'wwedite 3na4enie pogrewnosti='
read *,eps
do i=1,3
print *, 'wwedite 3na4enie a='
read *,a
print *,'wwedite 3na4enie b='
read *,b
if (f(a)*f(b)>0) then
print *,'kornei net'
else
call bisection (a,f,x,eps,b,n)
print *,'x=',x
print *,'f=',f(x)
print *, 'n=',n
end if
end do
enddo
end
2.
subroutine bisection (a,f,x,eps,b,n)
n=0
do while ((abs(f(x))>eps) .or. (abs(a-b)>eps))
n=n+1
x=(a+b)/2
if (f(x)*f(a)<0) then
b=x
else
a=x
end if
end do
end
3.
function f(x)
real f,x
f=x**3+4.81*x**2-7.37*x+0.55
end
Результаты:
X1=-6.044385
X2=7.871094E-02
X3=1.155664
Fortran: метод касательных.
Текст программы:
1.
program piupiupiupiu
real x,eps,fx,xn
integer n
eps=0.001
print *,'vvod korney'
do i=1,3
print *,'x='
read *,x
n=0
do
xn=x-f(x)/f1(x)
if (abs(x-xn)<=eps.and.abs(f(xn))<=eps) exit
x=xn
n=n+1
end do
x=xn
fx=f(x)
print *,'x=',x
print *,'f=',fx
print *,'n=',n
end do
end
2.
function f(x)
real f,x
f=x**3+4.81*x**2-7.37*x+0.55
end
3.
function f1(x)
real f1,x
f1=3*x**2+9.62*x-7.37
end
Результаты:
X1=-6.044371
X2=7.873945E-02
X3=1.155631
Fortran: zreal.
Текст программы:
1.
program piwpiw
use msimslms
parameter (n=3)
external f
real errabs,errrel,eps,eta,f,xg(n),x(n)
integer info(n)
print*,'wwedite 3 na4alnix priblijeni9'
read*,(xg(i),i=1,n)
errabs=0.001
errrel=0.001
eps=0.001
eta=0.001
itmax=100
call zreal(f,errabs,errrel,eps,eta,n,itmax,xg,x,info)
print*,'korni',(x(i), i=1,n)
print*,'znachenie functsii',(f(x(i)),i=1,n)
print*,'kol-vo iteratsiy',(info(i),i=1,n)
end
2.
function f(x)
real f,x
f=x**3+4.81*x**2-7.37*x+0.55
end
Результаты:
X1=-6.04437
X2=7.873943E-02
X3=1.155631
Выводы:
1) При вычислении корней нелинейного уравнения средствами Excel сами корни уравнения более наглядно можно посмотреть на графике функциит. Тем Excel и лучше.
2) Метод
половинного деления является довольно медленным, но всегда сходящимся к решению
задачи, так как на каждой итерации отрезок делится пополам и после n итераций
уменьшается в 2n раз.
3) Подпрограмма ZREAL выполняет поиск вещественных корней. Это наиболее точный
метод из всех.
4) Метод касательных заключается в том, что он приближенно заменяет функцию
f(x) касательной к ее графику в точке хn. Выбрав начальные приближения x0,
строится касательная к графику функции. Точка пересечения касательной с осью
абсцисс будет являться очередным приближением к корню и итерационный процесс будет выполняться до тех
пор, пока Ixn+1 – xnI < и If(xn)I<. Это точный, но сложный метод.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.