Численные методы решения нелинейных уравнений (с помощью Excel)

Лабораторная работа по информатике: «Численные методы решения нелинейных уравнений»

Выполнил: Гаврилин Дмитрий,                                                                         студент 421 группы

Цели работы: 1) С помощью Excel построить таблицу, график цункции и вывести результаты.

2) Найти значение Х, при котором функция достигает своего минимального значения с помощью метода «Золотого сечения»; найти значение функции в точке минимума; найти значение производной функции в точке минимума; определить, за какое число итераций функция достигает своего минимального значения.

3) Выводы.

Excel: построение таблицы, графика и вывод результатов.

x	y=f(x)
-7	-55,2
-6,8	-41,4
-6,6	-28,8
-6,4	-17,4
-6,2	-7,2
-6	1,9
-5,8	10,0
-5,6	17,0
-5,4	23,1
-5,2	28,3
-5	32,7
-4,8	36,2
-4,6	38,9
-4,4	40,9
-4,2	42,3
-4	43,0
-3,8	43,1
-3,6	42,8
-3,4	41,9
-3,2	40,6
-3	39,0
-2,8	36,9
-2,6	34,7
-2,4	32,1
-2,2	29,4
-2	26,5
-1,8	23,6
-1,6	20,6
-1,4	17,6
-1,2	14,6
-1	11,7
-0,8	9,0
-0,6	6,5
-0,4	4,2
-0,2	2,2
0	0,6
0,2	-0,7
0,4	-1,6
0,6	-1,9
0,8	-1,8
1	-1,0
1,2	0,4
1,4	2,4
1,6	5,2
1,8	8,7
2	13,1

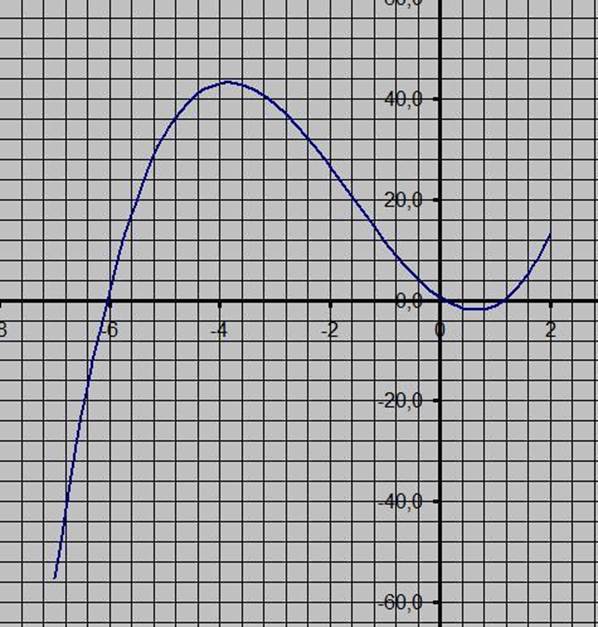
Экстремум	Значение экстремума	Значение функции
min	0,63884071	-1,9
max	-3,84550738	43,2

Метод золотого сечения.

Код пограммы:

1.

program se4enie

real x1,a,b,t,x,f,x2

external f

eps=0.001

t=(sqrt(5.)-1)/2

print*,'zna4enie t:',t

print*,'granitsi intervala a,b'

read*,a,b

x1=a+(1-t)*(b-a)

x2=a+t*(b-a)

do while (abs(a-b)>eps)

if (f(x1)<=f(x2)) then

b=x2

x2=x1

x1=a+(1-t)*(b-a)

else

a=x1

x1=x2

x2=a+t*(b-a)

end if

end do

x=(a+b)/2

print*,'3na4enie 3kstremuma:',x

print*,'3na4enie funkzii f(x):',f(x)

read*,a

end

2.

function f(x)

real f,x

f=x**3+4.81*x**2-7.37*x+0.55

end

Результаты:

Выводы:

Золотым делением отрезка называется деление отрезка на 2 части таким образом, что отношение большей части к меньшей равно отношению длины всего отрезка к большей части.

 =

Алгоритм поиска золотого сечения:

1)  Начальный интервал неопределённости (а₀,в₀) делим двумя точками (х₁,х₂) по правилу золотого сечения х₁=а₀+(1-t)*(в₀-а₀)

х₂= а₀+t*(в₀-а₀)

t= » 0,618

2)  Вычисляем значение функции в точках х₁ и х₂

y₁=f(х₁)       y₂=f(х₂)      

3)  Если y₁< y₂, очевидно точка минимума расположена на отрезке (а₀,х₂), поэтому (х₂,в₀) отбрасываем, сузив тем самым интервал неопределённости. На отрезке (а₀,х₂) снова выбираем две точки, но одна точка осталась от предыдущего деления, поэтому достаточно выбрать одну точку и рассчитать в ней значение функции а₁=а₀       в₁=х₂     х₂=х₁

4)  Если y₁> y₂, очевидно точка минимума расположена на отрезке (х₁,в₀) и тогда а₁=х₁       в₁=в₀     х₁=х₂

5)  Следуя разработанной схеме находим отрезки (а₂,в₂), (а₃,в₃) и т.д.

Процесс оптимизации повторяется до тех пор, пока Ia_n-b_nI≤eps

В качестве решения задачи принимается либо середина последнего интервала неопределённости, либо правая или левая граница.

Метод является медленным, но всегда сходящимся к решению задачи.