Сложные виды повреждений. Двойное замыкание на землю. Однофазное КЗ с разрывом фазы

                         10. Сложные виды повреждений

10.1.Общие замечания

        Сложные виды повреждений представляют собой совокупность нескольких несимметричных замыканий или нарушений продольной несимметрии отдельных участков системы. Возможны случаи, когда в системе одновременно возникают как поперечные, так и продольные несимметрии в самых различных комбинациях.

        Практический интерес обычно представляет одновременное нарушение симметрии лишь в двух точках системы, так как более сложные повреждения являются редкими исключениями. Поэтому в дальнейшем рассмотрена лишь двукратная несимметрия, причем предполагается, что обе несимметрии возникают практически одновременно.

         Рассмотрим основные принципы расчета таких повреждений. Их конкретное применение показано на двух наиболее часто встречающихся случаях: при двойных замыканиях на землю в сети с изолированной нейтралью и при однофазном КЗ с одновременным разрывом фазы.

10.2. Двойное замыкание на землю

        Предположим в произвольных точках М и N сети, работающей с изолированной нейтралью, произошли одновременные замыкания на землю фаз В и С (рис.10.1,а). При этом для упрощения примем, что оба замыкания являются металлическими, а все элементы сети – чисто индуктивными     Граничные условия в общих точках замыкания будут:

    I_MA = 0; I_MC = 0; U_MB = 0; I_NA = 0, I_NB = 0, U_NC = 0.                   (10.1)

Дополнительным условием является равенство: IMB=-INC                  (10.2)

Приняв неповрежденную фазу А за основную, запишем через симметричные составляющие следствия, которые вытекают из этих граничных условий:

            I_MB2 = I_MB1 или I_MA2 = a I_MA1,

            I_M0 = I_MB1 или I_M0 = a² I_MA1,

             U_MB1 + U_MB2 + U_M0 = a² U_MA1 + a U_MA2 + U_M0               ( 10.3)    

                                             I_NC2 = I_NC1 или I_NA2 = a² I_NA1,

                                                 I_N0 = I_NC1 или I_N0 = a I_NA1,

                                     U_NC1 + U_NC2 + U_N0 = a U_NA1 + a² U_NA2 + U_N0 = 0,

и, наконец, из (10.2) в соответствии с (10.3):

                                      I_NA1 = -aI_MA1.                                        (10.4)

         Равенство (10.4) показывает, что симметричные составляющие токов в обоих местах замыкания не являются независимыми переменными, а находятся в жесткой связи между собой, как это наглядно иллюстрируют векторные диаграммы на рис. 10.2.

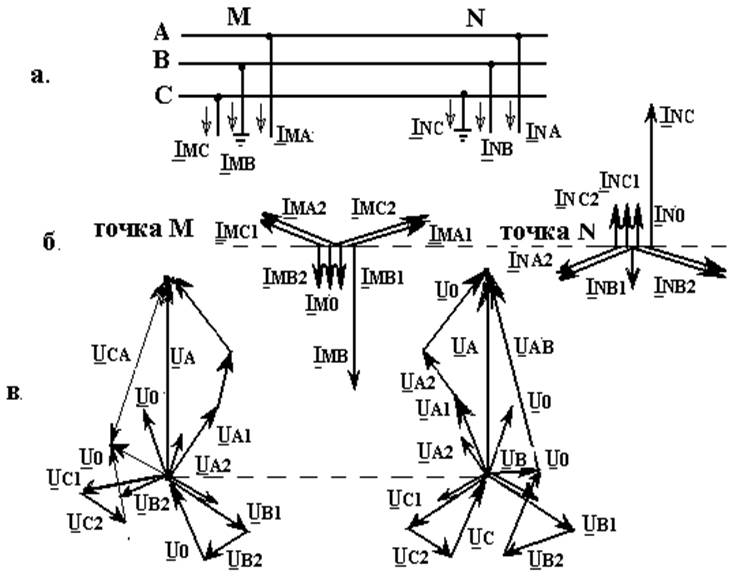
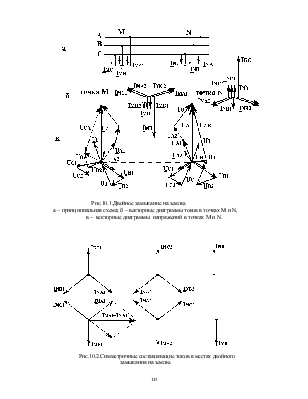
                       Рис.10.1.Двойное замыкание на землю.

а – принципиальная схема; б – векторные диаграммы токов в точках M и N,

                       в –  векторные диаграммы  напряжений в точках М и N.

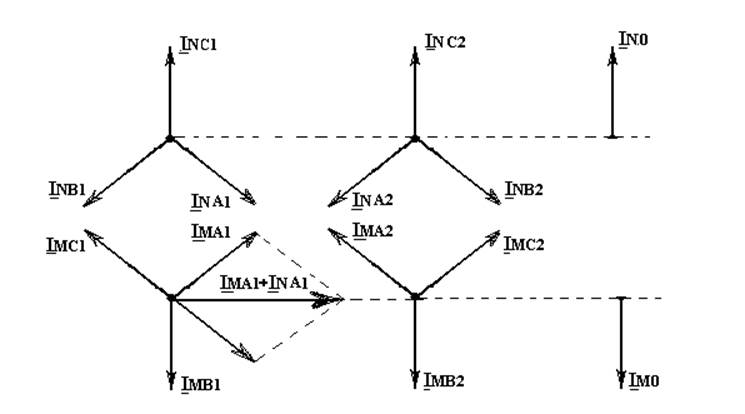
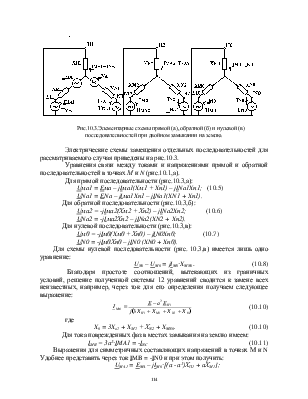
                  Рис.10.2.Симметричные составляющие токов в местах двойного                                             

                                               замыкания на землю.

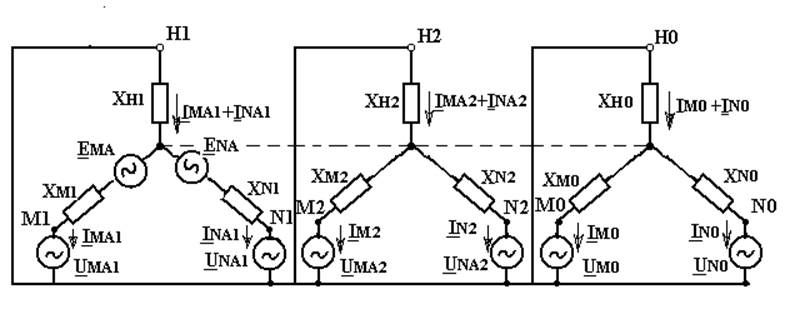
Рис.10.3.Элементарные схемы прямой (а), обратной (б) и нулевой (в)                                последовательностей при двойном замыкании на землю.

       Электрические схемы замещения отдельных последовательностей для рассматриваемого случая приведены на рис.10.3.

       Уравнения связи между токами и напряжениями прямой и обратной последовательностей в точках М и N(рис.10.1,а).

       Для прямой последовательности (рис.10.3,а):

Uмa1 = Eмa – jIмa1(Xм1 + Xн1) – jINa1Xн1;   (10.5)

              UNa1 = ENa – jIмa1Xн1 – jINa1(XN1 + Xн1).

     Для обратной последовательности (рис.10.3,б):

              Uма2 = -jIма2(Хм2 + Хн2) – jINa2Xн2;            (10.6)

UNa2 = -jIма2Хн2 – jINa2(XN2 + Xн2).

     Для нулевой последовательности (рис.10.3,в):

              Uм0 = -jIм0(Xм0 + Хн0) – jIN0Xн0;                (10.7)

              UN0 = -jIм0Хн0 – jIN0 (XN0 + Xн0).

Для схемы нулевой последовательности (рис. 10.3,в) имеется лишь одно уравнение:

           U_N0 – U_M0 = jI_M0·X_MN0.                                   (10.8)

        Благодаря простоте соотношений, вытекающих из граничных условий, решение полученной системы 12 уравнений сводится к замене всех неизвестных, например, через ток для его определения получаем следующее выражение:

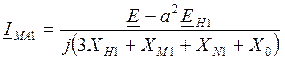                                  (10.10)

       где

    X₀ = 3X_н2 + X_М2 + Х_N2 + X_MN0.                                            (10.10)  

     Для тока поврежденных фаз в местах замыкания на землю имеем:

           I_МВ = 3а²·IMA1 = -I_NC                                                             (10.11)

Выражения для симметричных составляющих напряжений в точках М и N Удобнее представить через ток IMB = -IN0 и при этом получить:

                                     U_MA1 = E_MA – jI_M0·[(a - a²)X_Н1 + аХ_М1];

                                          U_MA1 = jI_M0·[(a² - a)X_Н2 + а²Х_М2];

                              U_M0 = -(a²U_MA1 + aU_MA2);                               (10.12)

                                      U_NA1 = E_NA – jI_M0·[(a - a²)X_н1 - a²X_N1];

                                          U_NA2 = -jI_M0·[(a² - a)X_Н2 – aX_N2];

                                                U_N0 = -(aU_NA1 + a²U_NA2).