Сложные виды повреждений. Двойное замыкание на землю. Однофазное КЗ с разрывом фазы, страница 3

10.3.Однофазное КЗ с разрывом фазы

   Рассмотрим случай, когда одновременно возникают поперечная и продольная несимметрия.

   Пусть на каком – либо участке сети, нейтраль которой заземлена, произошел разрыв одного провода, причем один конец провода заземлился, а другой остался изолированным (рис.10.5). Питание данного участка предполагается с обеих его сторон.

     Граничные условия будут:

I_кВ = 0; I_LA = 0; I_kC = 0; ∆U_LB = 0; U_kA = 0; ∆U_LC = 0.               (10.17)

Основные уравнения:

                                  U_LA1 = E_LA – jI_LA1(X_L1 + X_Н1) - jI_L˙A1X_Н1;  

U_L˙A1 = E_L˙A – jI_LA1X_Н1 - jI_L˙A1(X_L˙ + X_Н1);

U_LA2 = -jI_LA2(X_L2 + X_Н2) - jI_L˙A2X_Н2;                        (10.18)                                   

U_L˙A2 = -jI_LA2X_Н2 - jI_L˙A2(X_L˙2 + X_Н2);   

U_L0 = -jI_L0(X_L0 + X_Н0) - jI_L˙0X_Н0;                                                 

U_L˙0 = -jI_L0X_Н0 - jI_L˙0 (X_L˙0 + X_Н0).

      Используя (10.17) и (10.18), получим дополнительную связь между неизвестными токами и напряжениями прямой последовательности в местах несимметрии:

                                              ∆U_LA1 = jX_kI_kA1 + jX_kLI_LA1;

                                            ∆U_LA1 = jX_kLI_kA1 + jX_LI_LA1,

       где X_k = X_k2 + X_k0 + (X_kL2 – X_kL0)² / (X_L2 + X_L0);                   (10.110)

                                          X_L = X_L2X_L0 / (X_L2 + X_L0);

X_kL = (X_kL2 X_L0 + X_kL0 X_L2) / (X_L2 + X_L0),

где Х_К2, Х_К0 – реактивности схемы соответствующей последовательности относительно точки КЗ при полном разрыве схемы в точке L;

Х_L2, Х_LO – то же относительно места разрыва при отсутствии КЗ;

Х_KL2, Х_KLO – взаимные реактивности между точкой КЗ и местом разрыва в схемах соответствующих последовательностей.

       Придадим уравнениям (10.18) несколько иной вид, введя в правую часть каждого уравнения два  oдинаковых, но противоположных по знаку слагаемых:

                                      U_kA1 = jX_kI_kA1 + jX_kLI_LA1 ± jX_kLIkL1 =

                 = j(X_k – X_kL) I_kA1 +jX_kL (I_kA1 + I_LA1);                       (10.20)        

                                      U_LA1 = jX_kL I_kA1 + jX_LI_LA1 ± jX_kL I_LA1 =

                                      = jX_kL (I_kA1 + I_LA1) + j(X_L + X_k1) I_LA1.

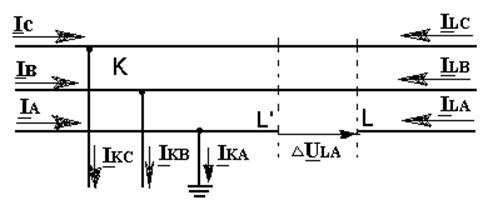
                Рис.14.5.Однофазное КЗ с одновременным разрывом той же фазы.

       Уравнениям (10.20) соответствует схема замещения, представленная на рис.10.6, из которой следует, что при рассматриваемой двукратной несимметрии расчетов токов и напряжений прямой последовательности (при ранее принятых допущениях) сводится к расчету эквивалентного КЗ в некоторой точке С, связанной с точками К1 и L1 схемы прямой последовательности реактивными сопротивлениями Х_KL, (Х_К – Х_KL) и  (Х_L – Х_KL), величины которых согласно (10.20) определяются реактивными сопротивлениями только схем обратной и нулевой последовательностей.

Таким образом, в данном случае соблюдается правило эквивалентности прямой последовательности со всеми вытекающими из него следствиям.

         Нужно отметить, что на схеме рис. 10.6 за положительное направление тока I_LA1 принято направление от места замыкания. Чтобы увязать с обычно принимаемым условием, что токи имеют положительное направление к точке КЗ, необходимо у найденного тока I_LA1изменить знак.

Напряжение прямой последовательности в месте КЗ относительно нулевого провода и относительно оборванного конца фазы    (ΔU_LA1)   определяются суммой соответствующих падений напряжений в схеме рис.10.6.

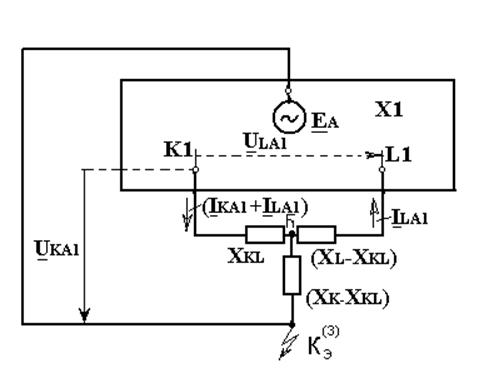
              Рис.10.6.Схема прямой последовательности для случая однофазного

                              КЗ с одновременным разрывом той же фазы.

Остальные симметричные составляющие токов и напряжений в местах несимметрии определяются из соотношений, которые вытекают из граничных условий и уравнений связи (10.5) и (10.6).