Сложные виды повреждений. Двойное замыкание на землю. Однофазное КЗ с разрывом фазы, страница 4

        Распределение токов и напряжений находят обычными приемами или с использованием принципа наложения.

        Если приведенные ЭДС источников равны между собой и параметры схем прямой и обратной последовательностей принять одинаковыми, то для определения тока прямой последовательности в месте КЗ при одновременном разрыве той же фазы с одной стороны можно получить расчетное выражение:

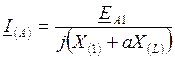                                 .                                                   (10.21)

где Х₍₁₎ = 2Х₁ + Х0 – результирующая реактивность при однофазном КЗ в точке К и отсутствии разрыва фазы в точке L;

,

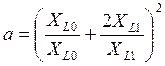
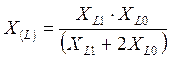     где Х_L1 и X_KL1 – то же, что ранее Х_L2 и Х_KL2

        Из структуры выражения (10.21) непосредственно видно уменьшение тока КЗ, вызванного одновременным разрывом поврежденной фазы с одной стороны.

 ПРИМЕР 10.1. При двойном замыкании на землю в точках М и N схемы рис.10.7,а определить фазные токи линии и обеих трансформаторов (на стороне, где произошло замыкание), а также фазные напряжения в местах замыкания. Результаты представить векторными диаграммами. Расчет произвести для начального момента, считая, что генератор предварительно работал на холостом ходу с номинальным напряжением.

              Генератор G 37,5 МВ·А; 6,3кВ; Х"d* = 0,143 = X1 = X2;

              Трансформатор Т – 1 25МВ·А; 37/6,3 кВ; Uк = 8%; У/∆– 11;

              Трансформатор Т – 2 40МВ·А 115/37/10,5 кВ; U_BC = 10,5%; У/∆;

              Линия W 12,5 км; Х1 = 0,4 Ом/км; Хо = 1,45 Ом/км.

          Система GC – источник бесконечной мощности (Х1 = Х2 = Х0 = 0) с напряжением 115 кВ.

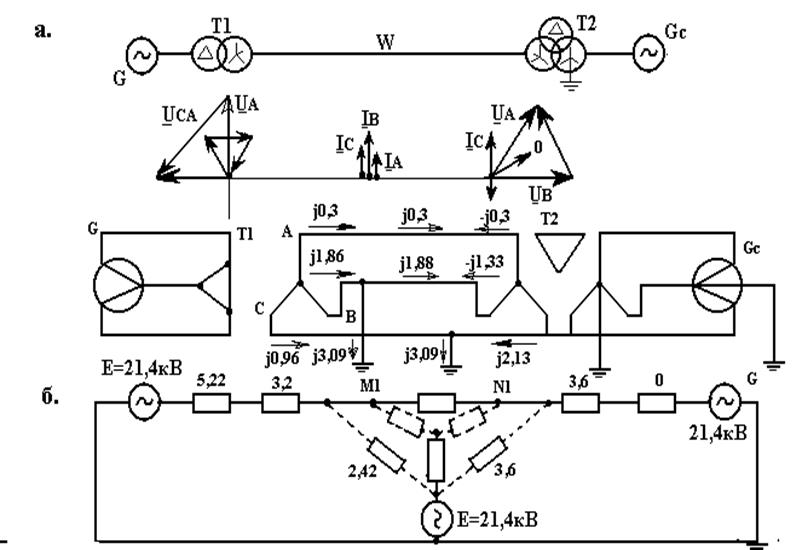
На рис.10.7,б показана схема замещения прямой последовательности, где указаны реактивные сопротивления (Ом) всех элементов и ЭДС (кВ) источников. После исключения ЭДС, получившаяся схема является схемой замещения обратной последовательности. Схема нулевой последовательности (рис.10.7,в) содержит только один элемент – линии.

Решение проведем в именованных единицах, относя все элементы к стороне линии

                             Рис.10.7. К примеру 10.1

а – исходная схема; распределение токов, векторные диаграммы токов и                                                   напряжений; б – схема замещения прямой (обратной) последовательности. в – то же нулевой последовательности.

Объединив начала генерирующих ветвей, получим треугольник, преобразование которого в звезду (пунктир на рис.10.7,б) дает реактивные сопротивления схем прямой, обратной и нулевой последовательностей   ХМ1 = ХM2 = 2,47 Ом, ХN1 = 2,47 Oм, ХN1 = XN2 = 1,06 Oм, ХН1 = ХН2=1,78 Ом.

                 Х0 = 3·1,78 + 2,47 + 1,06 + 1,81 = 27 Ом.

Принимая  Еа = j 21,4 кВ, для тока прямой последовательности

имеем: IMA1 = (1-a²)21,4/j(31,78 + 2,47 + 1,06 + 27) = 1,03<30град  и для токов других последовательностей:  IMA2 = a IMA1 = 1,03<150град, кА,

        IM0 = a² IMA1 = -j 1,03 кА.

Найдем распределение токов, для чего предварительно определим необходимые коэффициенты распределения:

       С(М) = (3,6 + 5) / (8,42 + 3,6 + 5) = 0,505, С(N) = 3,6 / 17,2 = 0,21,

и со стороны трансформатора Т – 2:

                                            С(М) = 1 – 0,505 = 0,4105;

                                            С(N)  = 1 – 0,211 = 0,789.

Эти коэффициенты справедливы и для схемы обратной последовательности. Поскольку при отсутствии замыканий тока в линии нет (пренебрегая емкостным током), фазные токи трансформатора Т – 1 с учетом того, что здесь I0 = 0, будут:   IA = - (0,505 – 0,211)(-j 1,03) = 0,3 кА;

                                                IB = (2 0,505 + 0,211)(-j 1,03) = -j 1,26 кА;

                                                IC = - (0,505 + 2 0,211)(-j 1,03) = j 0,106 кА.

       Для фазных токов линии имеем:

               IA = j 0,3кA; IB = -j 1,26 + j 3,010 = j 1,83 кA; IC = j 0,106 кA.