Сложные виды повреждений. Двойное замыкание на землю. Однофазное КЗ с разрывом фазы, страница 2

         На рис.10.1,б,в,г приведены векторные диаграммы токов и напряжений в местах двойного замыкания на землю. Диаграммы напряжений показывают, что величина и сдвиги фазных напряжений зависят от соотношения между реактивными сопротивлениями элементарных схем отдельных последовательностей (рис.10.3,б,в,г). Контролем правильности расчета может служить соблюдение условия, что в чисто индуктивной цепи угол между током Iмо и разностью напряжений (U_NO – U_MO) должен быть 100 эл.град.

     После того, как найдены симметричные составляющие токов и напряжений в местах двойного замыкания на землю, их распределение в схемах соответствующих последовательностей можно найти обычным путем. Поскольку симметричные составляющие одноименной последовательности в обеих точках несимметрии сдвинуты друг относительно друга (а в схеме прямой последовательности и по отношению к ЭДС), то, несмотря на однородный характер сопротивлений элементов схемы, расчет токораспределения требует операций с комплексными числами.

        При данном виде двойной несимметрии токораспределение значительно проще найти, применяя наложения. Для этого, считая схемы всех последовательностей пассивными, следует найти распределение тока каждой последовательности IMI при INI = 0(i= 1,2,0), а затем, наоборот, распределение тока INI при IMI=0. Действительная величина тока каждой последовательности в произвольной ветви будет:

                    ,                                   (10.13)

где  ,   – коэффициенты распределения, найденные для данной ветви соответственно при I_Mi = 1, когда I_Ni = 0, и при I_Ni = 1, когда I_Mi = 0.

     Для получения тока прямой последовательности нужно к току найденному по (10.13) прибавить ток, проходящий по этой ветви при отсутствии обеих несимметрий.

     В большинстве практических расчетов двойного замыкания на землю принимают одинаковыми схемы прямой и обратной последовательностей, но в  схеме обратной последовательности отсутствуют ЭДС. При этом выражении для фазных токов любой ветви могут быть приведены к простому виду:

I_A = [C₀ – C_(M) – C_(N)] I_M0;

                                     I_B = [C₀ + (2C_(M) + C_(N))]I_M0;                            (10.14)

                                                I_C = [C₀ – (C_(M) + 2C_(N))] I_M0;              

где Со – коэффициент распределения для данной ветви в схеме нулевой     последовательности (считая I_Mo =- I_No = 1).

С_(M), С_(N) – те же коэффициенты, которые указаны выше; при принятом условии в схеме прямой и обратной последовательностей они одинаковы, поэтому индекс последовательностей опущен.

В общем случае к этим фазным токам нужно прибавить ток в той же ветви при отсутствии двойного замыкания.

Для практического определения тока прямой последовательности (а по нему и полного тока) в месте двойного замыкания на землю удобно использовать приближенную схему, представленную на рис. 10.4. Здесь каждая из точек двойного замыкания в схеме прямой последовательности (М₁ и N₁) соединена с точкой нулевого потенциала через реактивность:

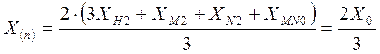                             .              (10.15)

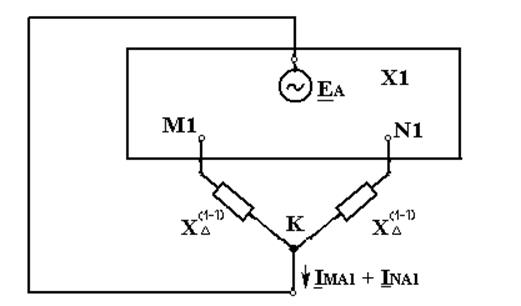
Рис. 10.4. Приближенная схема замещения для определения тока прямой

Последовательности при двойном замыкании на землю.

    При этом следует иметь в виду, что поскольку в такой схеме отсутствует сдвиг между токами I_MAI и I_NAI, она позволяет найти приближенное значение модуля суммы этих токов. Поэтому затем легко найти модули токов в каждом месте двойного замыкания, т.к. в соответствии с рис.10.3 имеем:

I_M1 = I_N1 = I_MA1 + I_NA1/√3.                                        (10.16)

     Ошибка, обусловленная применением указанной приближенной схемы, обычно не превышает 5…10%. Преимущество этой схемы при расчете двойного замыкания является возможность применения всех практических методов расчета переходного процесса КЗ в одной точке.