2.2 Определение математического описания управляющих устройств
Устройство, с помощью которого в системах регулирования обеспечивается автоматическое поддержание технологической величины около заданного значения, называют автоматическим регулятором. Регулятор является одним из элементов замкнутой системы.
На вход автоматического регулятора подаются текущее и заданное значения регулируемой величины. Рассогласование между ними приводит к изменению выходной величины регулятора. Эту зависимость в относительных величинах называют законом регулирования. Каждый конкретный регулятор имеет свой закон регулирования.
По закону регулирования регуляторы непрерывного действия делят на пропорциональные, пропорционально - дифференциальные, пропорционально – интегрально – дифференциальные и др.
2.2.1
Пропорциональный регулятор. Метод расчета пропорционального настроечного
коэффициента ![]()
К П-регуляторам относятся те, у которых выходная величина в пределах зоны регулирования изменяется пропорционально изменению входной величины.
Уравнение динамики П-регулятора имеет вид
![]() ,
,
где ![]() -
коэффициент передачи (пропорциональности) регулятора.
-
коэффициент передачи (пропорциональности) регулятора.
Каждому значению входной величины П-регулятора соответствует определенное значение выходной величины. Сигнал на входе П-регуляторов меняется только при изменении сигнала на входе. Структурная схема П-регулятора для исследования колонны для абсорбции показана на рис. 8.
 Q,
кг/ч Т,
Q,
кг/ч Т,
![]()
Рисунок 8 - Структурная схема
Алгоритм расчета
Рассчитывается
настройка П-регулятора ![]() по передаточной функции.
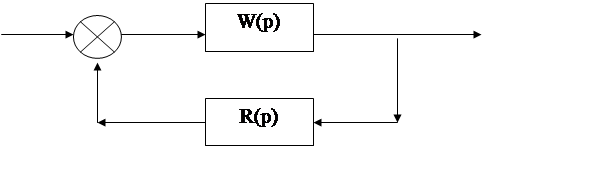
Заменим p на iw, то
по передаточной функции.
Заменим p на iw, то
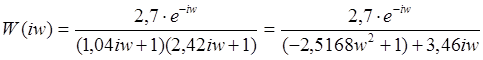 .
.
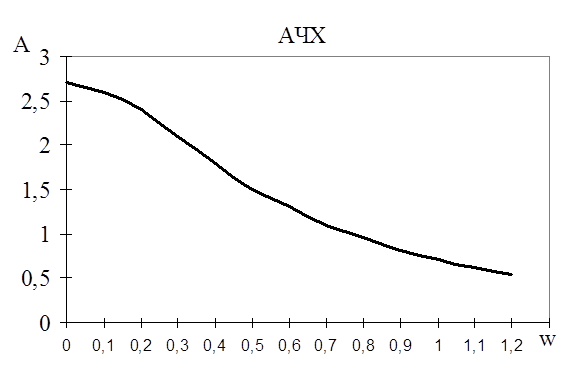
Строятся частотные характеристики объекта управления АЧХ и ФЧХ (рис. 9), которые раcсчитываются из формул (2) и (3) соответственно. Результаты расчетов сведены в таблицу 2.
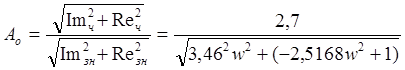 , (2)
, (2)
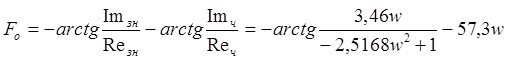 . (3)
. (3)
Таблица 2 - Результаты расчетов частотных характеристик
|
W |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
|
|
2,7 |
2,6 |
2,4 |
2,1 |
1,8 |
1,5 |
1,3 |
1,11 |
0,95 |
0,82 |
0,71 |
0,62 |
0,55 |
|
|
0 |
-25 |
-49 |
-68 |
-87 |
-106 |
-120 |
-135 |
-148 |
-160 |
-171 |
-181 |
-191 |
 |
||||||
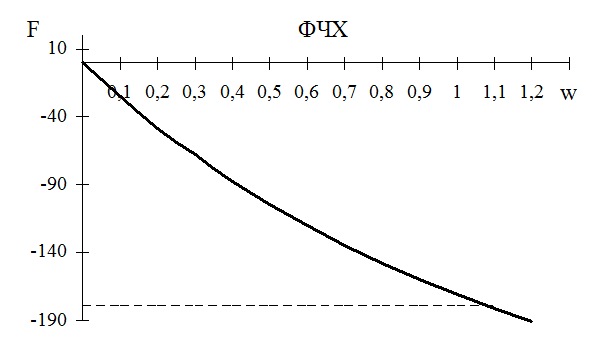
Рисунок 9 - Частотные характеристики объекта управления
Для данной
системы управления составляем систему уравнений Найквиста-Михайлова ![]() , где
, где ![]() - модуль
объекта,
- модуль
объекта, ![]() - модуль управляющего устройства:
- модуль управляющего устройства:
ì ![]()
![]() ì
ì![]()
í Û í (4)
î ![]() î
î![]()
т.к. y(t) = ![]() x(t),
x(t),
![]() (p) =
(p) = ![]() ,
,
![]() (w) =
(w) = ![]() ,
,
![]() (w) = 0.
(w) = 0.
Решением второго уравнения из системы (4) является точка пересечения двух графиков: ФЧХ объекта управления и прямой на уровне p (-p).
Определяем
рабочую частоту системы путем проекции точки пересечения на ось w (рис. 5): ![]() = 1,09.
= 1,09.
Согласно
рабочей частоте ![]() определяется рабочая
амплитуда системы
определяется рабочая
амплитуда системы ![]() = 0,63.
= 0,63.
Из первого
уравнения системы уравнений (4) находим значение коэффициента
пропорциональности ![]() .
.
ì![]() ì
ì![]() = 1/
= 1/![]() ,
,
í
Û í
Þ ![]() = 1/0,63
= 1,6.
= 1/0,63
= 1,6.
î![]() î
î![]()
![]()
![]() 2.2.2
Пропорционально-интегральный регулятор. Метод расчета
пропорционально-интегральных настроечных коэффициентов
2.2.2
Пропорционально-интегральный регулятор. Метод расчета
пропорционально-интегральных настроечных коэффициентов ![]() и
и
![]()
Выходная величина ПИ-регулятора изменяется под действием пропорциональной и интегральной составляющих. Уравнение динамики ПИ-регулятора имеет вид
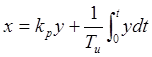 ,
,
где ![]() -
коэффициент передачи регулятора;
-
коэффициент передачи регулятора; ![]() – время интегрирования.
ПИ-регулятор имеет два параметра настройки.
– время интегрирования.
ПИ-регулятор имеет два параметра настройки.
Алгоритм расчета
Составляем систему уравнений Найквиста-Михайлова для конкретных исходных данных.
ì ![]() ì
ì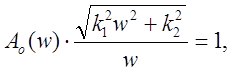
í Û í , (5)
î ![]() î
î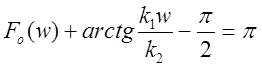
т.к. y(t) = ![]() x(t) +
x(t) + ![]()
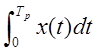 ,
,
y(p) = ![]() x(p) +
x(p) + ![]()
![]() x(p),
x(p),
![]() (p) =
(p) = ![]() +
+![]() =
=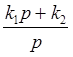 ,
,
![]() =
= 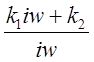 ,
,
![]() (w) =
(w) = 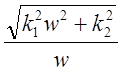 ,
,
![]() (w) =
(w) = 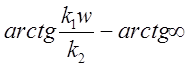 =
= 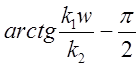 .
.
Согласно системе уравнений (5) строится плоскость
настроек пропорционально-интегральных коэффициентов ![]() и
и ![]() (рис.
10).
(рис.
10).
Плоскость настроек – это графическая зависимость интегральной настройки регулятора от пропорциональной; это экстремальная кривая, максимум которой соответствует минимуму среднеквадратичного критерия качества.
Алгоритм
построения плоскости настроек. Зададимся любым значением частоты ![]() . Подставив его в систему уравнений (5)
находим
. Подставив его в систему уравнений (5)
находим ![]() и
и ![]() .
Зададимся приращением
.
Зададимся приращением ![]() и новое значение частоты опять
подставим в систему уравнений (5) и т.д. до тех пор пока кривая не получит
перегиб и не будет найдено
и новое значение частоты опять
подставим в систему уравнений (5) и т.д. до тех пор пока кривая не получит
перегиб и не будет найдено ![]() . Результаты расчетов
сведены в таблице 3.
. Результаты расчетов
сведены в таблице 3.
Таблица 3 - Расчетные данные для построения плоскости настроек
|
|
0 |
0,50 |
0,6 |
0,65 |
0,70 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
1 |
|
|
0 |
0,10 |
0,27 |
0,39 |
0,52 |
0,65 |
0,83 |
0,98 |
1,13 |
1,23 |
1,40 |
|
|
0 |
0,33 |
0,43 |
0,48 |
0,51 |
0,52 |
0,51 |
0,48 |
0,41 |
0,32 |
0,22 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.