Определение математического описания управляющих устройств, страница 3

Задаются любым значением  и уравнения решаются относительно двух неизвестных. Пусть k1 = 0,8, то k2 = 0,61; k3 = 0,6.

Полученные числовые значения вставляются в комплекс:

0,25 <  k2*k3/k1^2 < 0,75;

0,25 < 0,59 < 0,75.

Полученные числовые значения настроечных коэффициентов для ПИД-регулятора неравенство удовлетворяют, поэтому расчет можно окончить.

2.3 Выводы

В данной главе по аналитическому методу расчета объекту управления был присвоен второй порядок и была найдена передаточная функция объекта по экспериментально снятой временной характеристике:

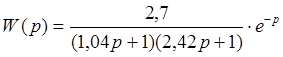
Были определены математические описания управляющих устройств:

-  для П-регулятора R(p) = 1,6;

-  для ПИ-регулятора R(p) = 0,45 + 0,5/p;

-  для ПИД-регулятора R(p) = 0,8 + 0,61/p + 0,6p.

2.3.1  Метод расчета П-закона регулирования

Исходные данные:

1)  математическая модель объекта

W₀(p)= )=[] exp(-7,8p)

2) математическая модель регулятора Х_р(t)=k₁z(t)

3) критерий устойчивости Найквиста-Михайлова W₀W_р+1=0

По известной W₀(p) находим амплитудно-частотную характеристику объекта и фазо-частотную характеристику объекта. Для этого заменяем pi, exp(-p)=cos-isin

W(i)=[]=[]

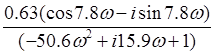A()=

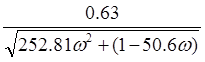
F()=-7,8-arctg()

Таблица 3 – значения АЧХ и ФЧХ от ω

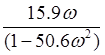	0	0,001	0,005	0,01	0,02	0,03	0,05	0,07	0,08	0,1	0,2	0,3	0,5	0,7	0,9	1,5	2
A	0,63	0,63	0,62	0,62	0,61	0,59	0,53	0,47	0,42	0,38	0,19	0,11	0,04	0,02	0,01	0,005	0,003
F	0	-1	-5	-9	-18	-27	-43	-56	-63	-74	-109	-129	-150	-160	-167	-179	-186

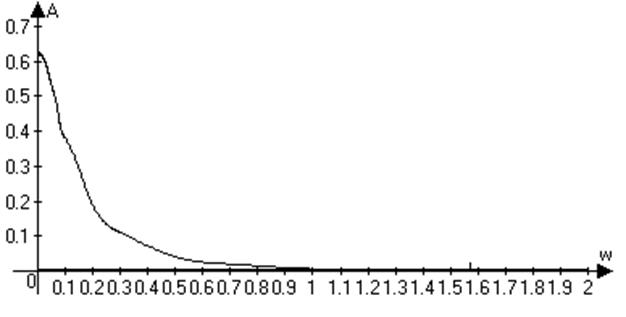
Рисунок 17-амплитудная характеристика

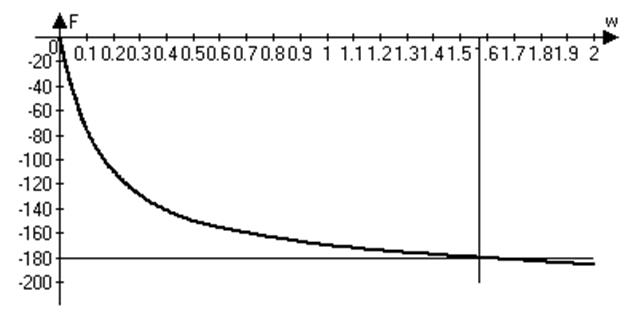
Рисунок 18-частотная характеристика

Критерий Найквиста-Михайлова представляем в алгебраической форме:

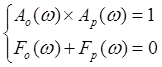
      =1,57, A_o(ω_p)=0.005

Зная ω_р и А_о(ω)А_р(ω)=1, можно определить значение АЧХ регулятора для этой рабочей ω.

А_р(ω_р)=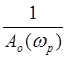=k₁;  k₁=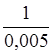=200

R(p)=200

2.3.2  Метод расчета ПИ-закона регулирования

Исходные данные:

1)  Математическая модель объекта W_o(p)

2)  Математическая модель регулятора х_р=k₁z(t)+k₂

2.2.2.1)Задаем любые значения частоты и из АЧХ и ФЧХ объекта строим последовательность векторов.

Таблица 4 – значения АЧХ и ФЧХ при различных ω

	0,07	0,08	0,1	0,2	0,3	0,5
A	0,47	0,42	0,38	0,19	0,11	0,04
F	-56	-63	-74	-109	-129	-150

2.2.2.2) Из вершин векторов строим перпендикуляры.

2.2.2.3) На перпендикулярах откладываем отрезки, длины которых вычислили по формуле:

ω_iA_i=

где Оω_i – длина каждого i-ого вектора или АЧХ;

         ω_i – выбранная частота;

         Т_иi – время интегрирования, выбирается произвольно.

Таблица 5 – значения отрезков в зависимости от значений Т_и и ω_i

Ти                        ωi	ω1	ω2	ω3	ω4	ω5	ω6
1	6.71	5.25	3.8	0.95	0.37	0.08
2	3.36	2.63	1.9	0.48	0.18	0.04
3	2.24	1.75	1.27	0.32	0.12	0.03
4	1.68	1.31	0.95	0.24	0.09	0.02
5	1.34	1.05	0.76	0.19	0.07	0.016
6	1.12	0.88	0.63	0.16	0.06	0.013

2.2.2.4) На каждый перпендикуляр откладываем значения отрезков ωА, с соответствующей  ω

2.2.2.5) Точки соответствующие одинаковому значению времени интегрирования, но разным частотам, соединяем плавными кривыми

2.2.2.6) Из начала координат, под углом 38⁰ к отрицательной реальной оси, проводим луч ОЕ