Определение математического описания управляющих устройств, страница 5

–  среднеквадратичный критерий качества стремящейся к min

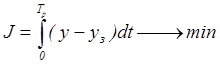                                                              (3.2)

–  динамический критерий, степень колебательности

т.к. в системе присутствуют электрические звенья, то m = 0,75.

Производим расчет параметров настройки регулятора одноконтурной САР аналитическим методом

Передаточная функция объекта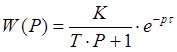.                                                                             (3.3) 

Получение расширенной АФХ объекта, осуществляется заменой Р на (-) в формуле передаточной функции объекта:

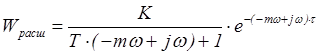,                                                  (3.4)

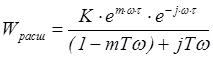.                                                                    (3.5)

                                                                 (3.6)

Получение расширенной АЧХ объекта

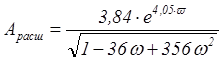                                                                    (3.7)

Получение расширенной ФЧХ объекта

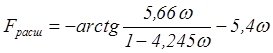                                                                  (3.8) 

Задаваясь любым значением частоты, находим А_расш и F_расш объекта и строим вектор объекта в комплексной плоскости.

Из систем уравнения Найквиста – Михайлова определяются параметры регулятора.

Полученные характеристики регулятора откладываются в комплексной плоскости (ДП 05 ВАЭ 1. 01. 06). Из характеристик или вектора регулятора определяются параметрические функции Jи R.

J – мнимая параметрическая функция, представляет собой проекцию вектора регулятора на мнимую ось

R – реальная параметрическая функция, представляет собой проекцию вектора регулятора на реальную ось

По двум последним формулам (3.7) и (3.8) производим расчеты и сводим в таблицу 3.1.

Таблица 3.1 - Расширенных характеристик и вычисление мнимых и реальных параметров функции.

Полученные числовые значения Jи Rв виде точки заносятся в плоскость параметрической функции (ДП 05 ВАЭ 1. 01. 06).

Задаваясь приращением частоты, строим плоскость параметрических функций до тех пор пока не будет найден max.

J_max= 0,05

R_max= 0,15

Составляем систему уравнений, которая отображает параметры только регулятора, для этого в передаточную функцию ПИД регулятора заносятся расширенное p.

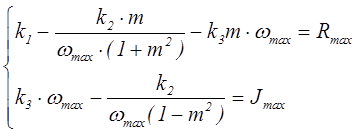                                        (3.9)

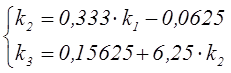                                                    (3.10)

Для решения системы уравнения (3.10) задаемся любым численным значением коэффициента k₁и решаем систему относительно k₂и k₃. Затем полученное значение подставляем в неравенство (3.11)

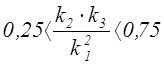                                                               (3.11)

Неравенство выполнено при следующих коэффициентах:

k₁ = 1

k₂ = 0,27

k₃ = 1,87

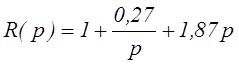
Литература

1.  Автоматизация настройки систем управления / В.Я. Ротач, В.Ф. Кузищин, А.С. Клюев и др.; Под ред. В.Я. Ротача. – М.: Энергоатомиздат, 1984. – 391 с.

2.  Клюев А.С., Лебедев А.Т., Новиков С.И. Наладка систем автоматического регулирования барабанных котлов. – М.: Энергоатомиздат, 1985. – с.

3.  Наладка средств автоматизации и автоматических систем регулирования: Справочное пособие / А.С. Клюев, А.Т. Лебедев, С.А. Клюев и др.: по ред. А.С. Клюева. – М.: Энергоатомиздат, 1989. – 368 с.

4.  Полоцкий Л.М., Лапшенков Г.И. Автоматизация химических производств. Теория, расчет и проектирование систем автоматизации. – М.: Химия, 1982. – 296 с.

5.  Ротач В.Я. Расчет настройки промышленных систем регулирования. – М. – Л.: Госэнергоиздат, 1961. – 344 с.

6.  Ротач В.Я. Расчет динамики промышленных автоматических систем регулирования. – М.: Энергия, 1973. – 440 с.

7.  Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами: Учебник для вузов. – М.: Энергоатомиздат, 1985. – 347 с.

8. Стефани Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. – М.: Энергия, 1972. – 376 с.