Определение математического описания управляющих устройств, страница 4

2.2.2.7) Строим касательные окружности, такие , чтобы их центр был на отрицательной реальной оси и они касались, как луча ОЕ, так и построенных кривых

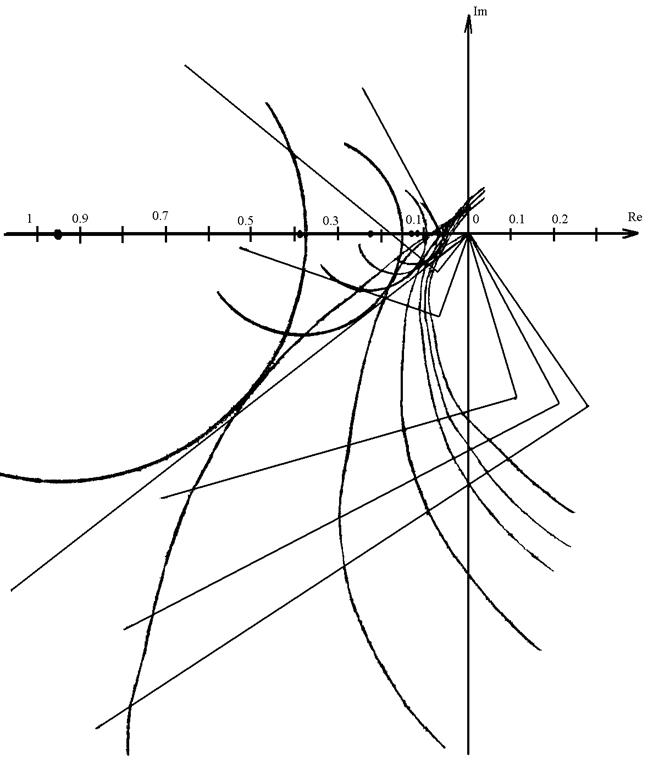
Рисунок 20 – амплитудно-фазо-частотная характеристика

Получили последовательность радиусов:

r₁=0.95, r₂=0.38, r₃=0.22, r₄=0.16, r₅=0.13, r₆=0.12

2.2.2.8) Находим пропорциональные настройки:

k₁¹==1.05, k₁²=2.63, k₁³=4.5, k₁⁴=6.25, k₁⁵=7.7, k₁⁶=8.3

2.2.2.9) Строим плоскость границы устойчивости в координатах рассчитанных k₁ и выбранных Т_и

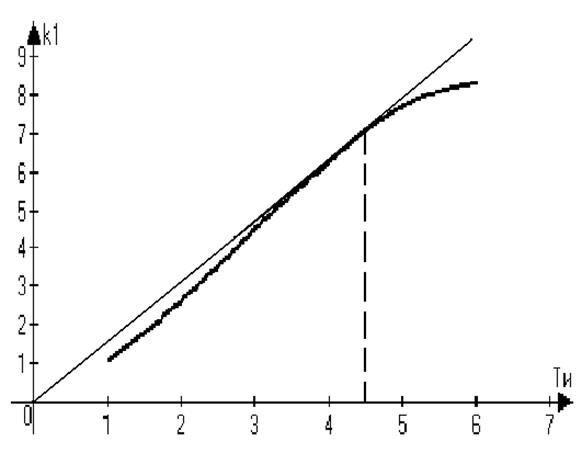
Рисунок 21-плоскость границы устойчивости

Построили касательную к плоскости устойчивости из начала координат, и точка касания будет определять оптимальные коэффициенты k₁^o и Т_и^о

k₁^o=7, Т_и^о=4,5

2.2.2.10) Находим числовые значения интегральной настройки регулятора

   k₂^o===0.22

R(p)=7+

2.3.3  Метод расчета ПИД-закона регулирования

Метод основан на применении критерия качества заданной степени колебательности.

1)  Составили расширенную характеристику объекта. Для этого в передаточной функции объекта

р iω-mω, Степень колебетельности m=0.75, так как регуляторы носят электрический характер или обладают электрической физической природой.

W=[]

W==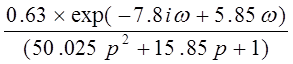

==

=

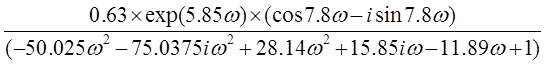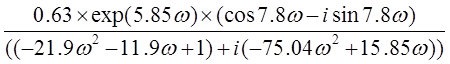
A=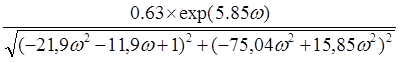

F=-7.8ω-arctg()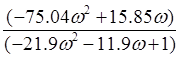

2)  Из АФХ расширенной, используя систему уравнений Найквиста-Михайлова, определили частотные характеристики регулятора по алгоритму:

1.1  Задали любые значения частоты ω_i ;

1.2  ω_i подставили в АЧХ объекта расширенное и ФЧХ объекта расширенное

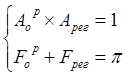
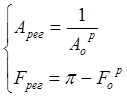
3)  Определили параметрическую функцию

I=A_рег sin F_рег

R= A_рег cos F_рег

Таблица 6 – значения АЧХ и ФЧХ при различных ω

ω	0.08	0.09	0.1	0.3	0.5	0.7
А	1.27	1.25	1.22	0.73	0.78	1.2
F	-97	-108	-117	-206	-230	-240
Ap	0.78	0.8	0.82	1.37	1.28	0.83
Fp	97	108	117	206	230	240
I	0.77	0.76	0.73	-0.6	-0.5	-0.72
R	-0.01	-0.25	-0.37	-1.23	-1.18	-0.42

4)  Из всех числовых значений I и R строится плоскость параметрической функции

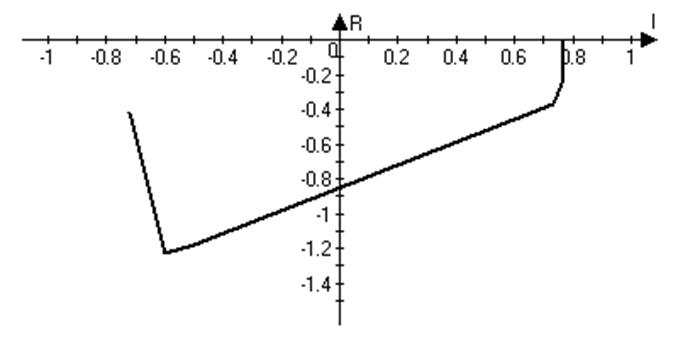
Рисунок 23-плоскость параметрической функции

ω_min=0.3, I_m=I^o= -0.6, R_m=R^o= -1.23

5)  Составили систему уравнений, которая отражает свойства только регулятора

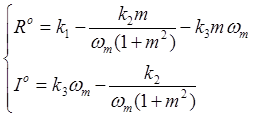
Задаем любые значения числовым коэффициентам k₁ и систему уравнений решаем относительно k₂, k₃. До тех пор пока не выполнится неравенство:

0,25<<0,75

k₁=30, 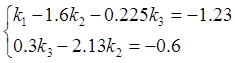      k₂=9.9, k₃=68.3

0.2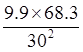5<<0.75найденные числовые значения являются оптимальными.

3.1 Расчет системы автоматического регулирования

Для расчета выбрана одноконтурная САР, в которой происходит автоматическое регулирование температуры в головках шприц-машин путем изменения расхода охлаждающей воды. (Необходимо обосновать выбор именно этой системы регулирования) В этом контуре регулирования применяем ПИД регулятор, т.к. он воздействует на объект регулирования прямопропорционально отклонению регулируемой величины интеграла отклонения и скорости отклонения. При скачкообразном изменении входной величины идеальный ПИД – регулятор в начальный момент времени оказывает мгновенное бесконечно большое воздействие на объект, затем величина воздействия мгновенно падает до значения определяемого пропорциональной частью регулятора, после чего вступает в работу ПИ - регулятор и воздействие на объект постепенно наращивается по интегральному закону.

Параметры регулятора – это пропорциональный коэффициент k₁, интегральный – k₂  и постоянный дифференциальный k₃.

ПИД – регулятор является универсальным т.к. задавая бесконечно большое или бесконечно малые значения коэффициентов можно получить регулирование любого типа.

Для проведения расчета необходимы следующие исходные данные:

–  динамические характеристики объекта;

–  динамические характеристики регулятора;

–  критерий устойчивости Найквиста – Михайлова в виде

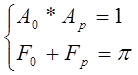                                    (3.1)