Определяем рабочую частоту системы:
т. к. ![]() = 0,75, то
= 0,75, то ![]() = 0,9
= 0,9![]() = 0,9·0,75 = 0,675.
= 0,9·0,75 = 0,675.
Рабочая частота подставляется в систему уравнений (4) и находятся оптимальные рабочие коэффициенты.
При w = 0,675 ![]() =1,15;
=1,15; ![]() = -132 Þ
= -132 Þ
![]() = 0,45 и
= 0,45 и ![]() =0,5.
=0,5.
![]()
![]()
![]()
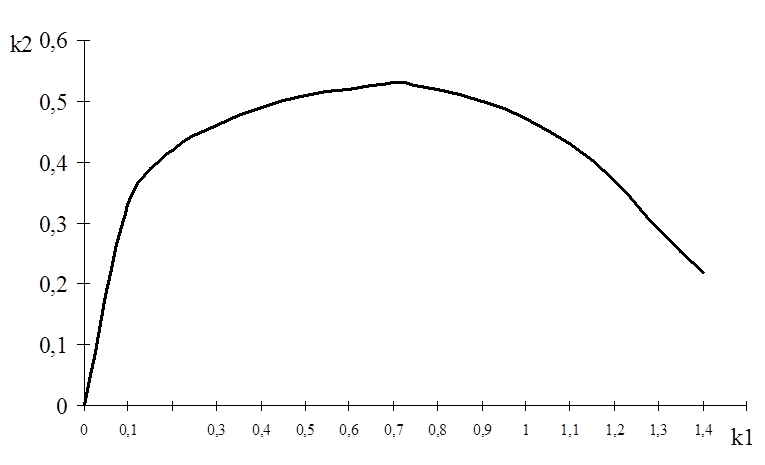 Рисунок
10 - Плоскость настроек ПИ-регулятора
Рисунок
10 - Плоскость настроек ПИ-регулятора
2.2.3
Пропорционально-интегрально-дифференциальный регулятор. Метод расчета
пропорционально-интегрально-дифференциальных настроечных коэффициентов ![]() ,
, ![]() и
и ![]()
В ряде случаев качество регулирования можно повысить введением в закон регулирования составляющей, пропорциональной первой производной или скорости изменения входной величины регулятора. Эта дифференцирующая составляющая формируется при помощи дополнительного устройства.
Уравнение динамики ПИД-регулятора имеет вид
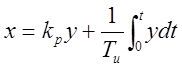 +
+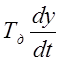 ,
,
где ![]() - коэффициент передачи регулятора;
- коэффициент передачи регулятора; ![]() – время интегрирования,
– время интегрирования, ![]() - время дифференцирования. ПИД-регулятор
имеет три параметра настройки.
- время дифференцирования. ПИД-регулятор
имеет три параметра настройки.
Алгоритм расчета
Для объекта управления составляется расширенная передаточная функция (-это искусственно измененная АФХ для придания системе устойчивости).
p ® -mw + iw, где m=0,75 – заданная степень колебательности.
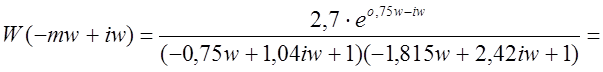
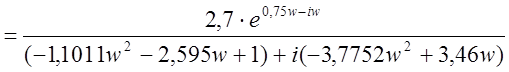 .
.
Определяем частотные характеристики объекта АЧХ и ФЧХ (табл. 4)
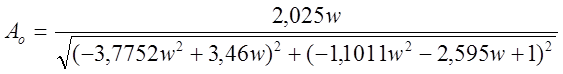 ,
,
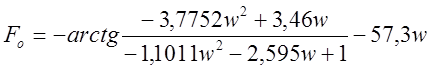 .
.
Определяем параметрические функции системы (см. табл. 4).
Существуют реальная параметрическая функция F и мнимая параметрическая функция j, которые выводятся путем расширения передаточной функции ПИД-регулятора.
т.к. y(t) = ![]() x(t) +
x(t) + ![]()
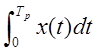 +
+ 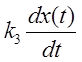 ,
,
y(p) = ![]() x(p) +
x(p) + ![]()
![]() x(p) +
x(p) + ![]() px(p)
px(p)
![]() (p) =
(p) = ![]() +
+![]() +
+![]() p=
p=![]() ,
,
![]() =
=![]() +
+![]() / (-mw+iw) +
/ (-mw+iw) + ![]() ·(-mw+iw),
·(-mw+iw),
![]() (w) =
(w) = 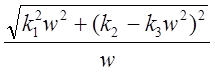 ,
,
![]() (w)
(w)  .
.
После преобразований получаем передаточную функцию регулятора в параметрическом виде
![]() (p) = F + mj - ij,
(p) = F + mj - ij,
где F = - ![]() + 2
+ 2![]() mw,
mw,
j = 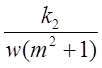 -
- ![]() w.
w.
Задаются
любым значением w и определяют вектор расширенной АФХ
объекта соответствующий этой частоте. Из вектора объекта определяется вектор
регулятора, угол поворота вектора регулятора противоположен по знаку вектору
объекта ![]() = -
= - ![]() , а
длина этого вектора определяется как
, а
длина этого вектора определяется как ![]() =1/
=1/ ![]() . Проекция w на
мнимую ось Im – это j,
проекция вектора регулятора на реальную ось Re – это Re = mj
+ F, т. е. F = Re - mj.
. Проекция w на
мнимую ось Im – это j,
проекция вектора регулятора на реальную ось Re – это Re = mj
+ F, т. е. F = Re - mj.
Таблица 4 - Расчетные данные для построения плоскости параметрических функций
|
W |
0 |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
|
|
2.7 |
0.12 |
0.26 |
0.42 |
0.58 |
0.73 |
0.86 |
0.94 |
1.00 |
1.03 |
1.04 |
|
|
0 |
-13.5 |
-28 |
-45 |
-62.5 |
-80 |
-97 |
-113 |
-128 |
-142 |
-155 |
|
|
0.37 |
8.72 |
3.91 |
2.40 |
1.72 |
1.36 |
1.17 |
1.06 |
1.00 |
0.97 |
0.96 |
|
|
0 |
13.5 |
28 |
45 |
62.5 |
80 |
97 |
113 |
128 |
142 |
155 |
|
Re |
0.37 |
8.48 |
3.45 |
1.70 |
0.79 |
0.24 |
-0.14 |
-0.41 |
-0.61 |
-0.76 |
-0.87 |
|
j |
0 |
2.04 |
1.84 |
1.70 |
1.53 |
1.34 |
1.16 |
0.97 |
0.79 |
0.60 |
0.40 |
|
F |
0.37 |
6.95 |
2.07 |
0.42 |
-0.36 |
-0.76 |
-1.01 |
-1.14 |
-1.20 |
-1.21 |
-1.17 |
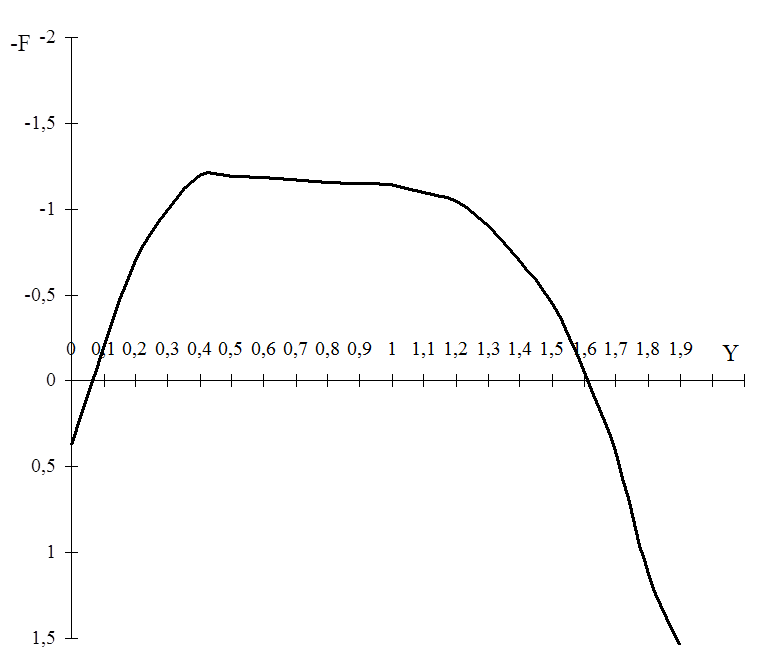 Строится плоскость параметрических функций
в координатах F(j)
(рис. 11) до тех пор пока кривая не получит перегиб и не будет найден
максимум, который соответствует минимуму среднеквадратичного критерия
качества. При
Строится плоскость параметрических функций
в координатах F(j)
(рис. 11) до тех пор пока кривая не получит перегиб и не будет найден
максимум, который соответствует минимуму среднеквадратичного критерия
качества. При ![]() = 0,45
= 0,45 ![]() =
-1,21;
=
-1,21; ![]() = 0,6.
= 0,6.
Рисунок 11 - Плоскость параметрических функций ПИД-регулятора
Составляем систему уравнений Найквиста-Михайлова с учетом полученных при расчете данных и решаем ее.
ì 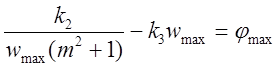 , ì
, ì ,
,
í Û í
î ![]() . î
. î ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.