Алгоритм
оценивания (5.1)-(5.6) получен минимизацией квадратичного функционала (3.9). Из
уравнения Риккати (5.2) и формул (5.3) и (3.5) следует, что матрица Гессе ![]() этой задачи оптимизации положительно
определена (либо положительно полуопределена) при любых значениях параметра
регуляризации
этой задачи оптимизации положительно
определена (либо положительно полуопределена) при любых значениях параметра
регуляризации ![]() , параметров
, параметров ![]() и
и ![]() ПИ-преобразователя
(3.5) и элементов
ПИ-преобразователя
(3.5) и элементов ![]() диагональной матрицы
диагональной матрицы ![]() нормирующих множителей. Поэтому
динамическая система (5.1)-(5.6) асимптотически устойчива и формирует
единственное решение рассматриваемой задачи оптимального управления [14]. Но
тогда из условия минимума следует, что переменные
нормирующих множителей. Поэтому
динамическая система (5.1)-(5.6) асимптотически устойчива и формирует
единственное решение рассматриваемой задачи оптимального управления [14]. Но
тогда из условия минимума следует, что переменные ![]() и
и ![]() обращают в нуль подынтегральное выражение
функционала (3.5). После подстановки выражений (5.5), (3.5) и (5.4) в (3.9) и
приведения подобных получим следующее уравнение для вектора
обращают в нуль подынтегральное выражение
функционала (3.5). После подстановки выражений (5.5), (3.5) и (5.4) в (3.9) и
приведения подобных получим следующее уравнение для вектора ![]() погрешностей управления:
погрешностей управления:
|
|
(5.7) |
Из теории
устойчивости Ляпунова известно, что решение линейного дифференциального
уравнения второго порядка с постоянными коэффициентами (5.7) устойчиво при
любых значениях параметров ![]() и
и ![]() ПИ-преобразователя (3.5). Поэтому отклонения
ПИ-преобразователя (3.5). Поэтому отклонения
![]() текущих значений переменных состояния ОУ,
формируемых с помощью ПИ-регулятора (5.1)-(5.6), от требуемых значений,
заданных формулами (1.6), (3.3) и (3.4), асимптотически уменьшаются до нуля
при
текущих значений переменных состояния ОУ,
формируемых с помощью ПИ-регулятора (5.1)-(5.6), от требуемых значений,
заданных формулами (1.6), (3.3) и (3.4), асимптотически уменьшаются до нуля
при ![]() . Требуемые (желаемые) законы изменения во
времени погрешностей управления
. Требуемые (желаемые) законы изменения во
времени погрешностей управления ![]() можно обеспечить
выбором числовых значений параметров
можно обеспечить
выбором числовых значений параметров ![]() и
и ![]() .
.
Пример
практической реализации. Качество полимеров, лаков, красок, машинных масел и
других нефтепродуктов определяют в процессе их производства по текущим значениям
плотности ![]() , кинематической вязкости
, кинематической вязкости ![]() при характерной температуре
при характерной температуре ![]() и индексу вязкости (или по текущим
значениям вязкости при характерной температуре и энергии внутримолекулярных
связей
и индексу вязкости (или по текущим
значениям вязкости при характерной температуре и энергии внутримолекулярных
связей ![]() ). В процессе синтеза указанных нефтепродуктов
их плотность
). В процессе синтеза указанных нефтепродуктов
их плотность ![]() , вязкость
, вязкость ![]() и
параметры функциональной зависимости вязкости от температуры непрерывно
изменяются. На нефтеперерабатывающих предприятиях и предприятиях химической
промышленности России контроль вязкости и индекса вязкости выпускаемой
продукции осуществляют один раз в смену с помощью лабораторных вискозиметров.
Управляют технологическими процессами синтеза этих продуктов с помощью автоматизированных
систем управления на основе опыта и интуиции оператора (аппаратчика). В
результате эти предприятия выпускают большое количество некондиционной продукции
[1]. Поэтому для
промышленных установок непрерывного производства были разработаны адаптивные
системы автоматического контроля и управления вязкости и энергии
внутримолекулярных связей полимеров [15], вязкости и индекса вязкости машинных
масел [13], реализующие алгоритм адаптивного управления (4.1)-(4.4),
(5.1)-(5.6).
и
параметры функциональной зависимости вязкости от температуры непрерывно
изменяются. На нефтеперерабатывающих предприятиях и предприятиях химической
промышленности России контроль вязкости и индекса вязкости выпускаемой
продукции осуществляют один раз в смену с помощью лабораторных вискозиметров.
Управляют технологическими процессами синтеза этих продуктов с помощью автоматизированных
систем управления на основе опыта и интуиции оператора (аппаратчика). В
результате эти предприятия выпускают большое количество некондиционной продукции
[1]. Поэтому для
промышленных установок непрерывного производства были разработаны адаптивные
системы автоматического контроля и управления вязкости и энергии
внутримолекулярных связей полимеров [15], вязкости и индекса вязкости машинных
масел [13], реализующие алгоритм адаптивного управления (4.1)-(4.4),
(5.1)-(5.6).
Шесть адаптивных
систем автоматического контроля и управления вязкости и энергии внутримолекулярных
связей полимеров с 1994 года находятся в эксплуатации на Заводе органического
синтеза Могилевского ПО «Химволокно» (Белоруссия). Наблюдатель переменных
состояния этих систем выполнен в виде адаптивного проточного вискозиметра, оснащенного
цифровым вычислительным блоком (контроллером). Через калиброванный участок
трубопровода (с диаметром условного прохода ![]() м.),
помещенного в теплообменник, с помощью шестеренчатого насоса регулируемой
производительности прокачивают расплав полимера (или его полуфабриката) под
давлением 100 бар при температуре (290-310) градусов Цельсия. Трубопровод
оснащен шестеренчатым расходомером; датчиком потерь давления
м.),
помещенного в теплообменник, с помощью шестеренчатого насоса регулируемой
производительности прокачивают расплав полимера (или его полуфабриката) под
давлением 100 бар при температуре (290-310) градусов Цельсия. Трубопровод
оснащен шестеренчатым расходомером; датчиком потерь давления ![]() на длине
на длине ![]() трубопровода;
датчиком давления
трубопровода;
датчиком давления ![]() за расходомером
и датчиком температуры
за расходомером
и датчиком температуры ![]() расплава полимера.
расплава полимера.
Процесс ламинарного течения расплава полимера в трубопроводе описывают уравнением гидродинамики:
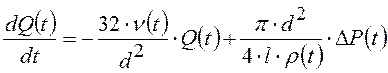 .
.
Математическая модель расходомера:
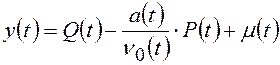
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.