Разработка и анализ алгоритма настройки параметров ПИ-регуляторов нелинейных систем управления, страница 2

где:  - заданная функция своих аргументов;  - погрешность управления;  - допустимая погрешность управления.

Для остальных переменных состояния ОУ в конечный момент времени управления должны выполняться условия:

Таким образом, формулами (1.1)-(1.7) задана априорная математическая модель системы управления. Уравнение (1.2) описывает математическую модель измерительных устройств. При этом предполагается, что динамическая система (1.1)-(1.2) наблюдаема и управляема, ограничения (1.3)-(1.7) совместимы, а конечное состояние (1.7) достижимо при выполнении всех ограничений.

Априорной информации, содержащейся в формулах (1.1)-(1.4) модели ОУ и ИУ при известных значениях вектора управляющих воздействий  в момент времени , достаточно для того, чтобы оценки  текущих значений переменных состояния ОУ  определить минимизацией функционала метода наименьших квадратов (МНК):

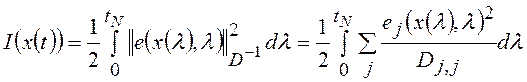
с учетом ограничений (1.1),(1.3), (1.4) где:  - вектор сигналов рассогласования между выходными сигналами ИУ и их оценкой, вычисленной с помощью математических моделей ОУ и ИУ:

 - положительно определенная диагональная матрица нормирующих множителей;  - квадрат предела абсолютной погрешности ИУ с номером .

При известных оценках текущих значений переменных состояния ОУ требуемые значения вектора управляющих воздействий  в момент времени можно определить минимизацией квадратичного функционала:

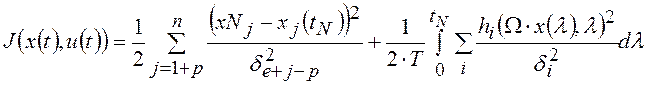
с учетом ограничений (1.1),(1.5) [5]. Однако при решении этой задачи условной оптимизации с помощью принципа максимума (либо с помощью динамического программирования) возникает нелинейная двухточечная краевая задача, которую нельзя решить в реальном времени в процессе управления.

2. Регуляризация исходной постановки задачи оценивания переменных состояния. Регуляризованную модель состояния ОУ будем определять в скользящем временном окне протяженностью . Изменение во времени параметров ОУ, возмущающих и управляющих воздействий будем описывать В-сплайнами с интервалом непрерывности сплайнов  [11]. Параметрами регуляризации при составлении такой модели ОУ являются порядок используемых сплайнов и интервал их непрерывности. При этом в задаче оценивания переменных состояния ОУ будем использовать значения управляющих воздействий , сформированные в момент времени  (В-сплайны нулевого порядка).

В веденном временном окне множество допустимых возмущающих воздействий (1.4) формирует вспомогательная динамическая система:

в которой используют В-сплайны нулевого порядка с интервалом непрерывности сплайнов , где:  – оценка возмущающего воздействия , определенная в момент времени ;  - корректирующее входное воздействие, подлежащее определению.

Множество непрерывных функций времени, заданных неравенствами (1.3), будем формировать с помощью В-сплайнов первого порядка:

и нелинейных преобразователей

с сигмоидальными статическими характеристиками:

гарантирующими выполнение ограничений (1.3), где  - корректирующее входное воздействие, подлежащее определению.

Тогда эволюцию во времени переменных состояния регуляризованной модели ОУ, объединенных в вектор , описывает нелинейное дифференциальное уравнение:

где:  - вектор  значений переменных состояния ОУ в момент времени  при действии управляющих воздействий , сформированных в момент времени ;

;

;  ;  .

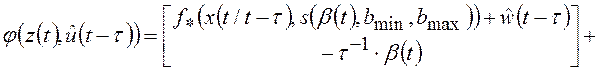
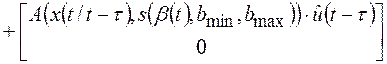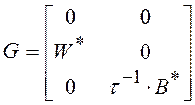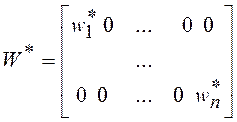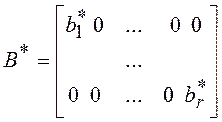В адаптивных системах управления оценки переменных состояния ОУ необходимо определять с учетом экспериментальной информации о прошлых и текущих значениях выходных сигналов измерительных устройств [3]. Такую информацию формирует из выходных сигналов измерительных устройств и регуляризованной модели ОУ (2.5) цифровой блок сравнения с ПИ-преобразователем (рис. 1).