где: ![]() - матрица дисперсий погрешностей
задания начальных условий;
- матрица дисперсий погрешностей
задания начальных условий; ![]() - положительно определенная
диагональная матрица нормирующих множителей, образованная, например, из
квадратов допустимых погрешностей управления
- положительно определенная
диагональная матрица нормирующих множителей, образованная, например, из
квадратов допустимых погрешностей управления ![]() ;
; ![]() -
параметр регуляризации.
-
параметр регуляризации.
Таким образом, исходная задача адаптивного управления с фиксированной правой границей с помощью методов регуляризации преобразована в нелинейную вариационную задачу со свободной правой границей: в задачу условной минимизации квадратичного функционала (3.10) при ограничении (3.9).
4. Синтез наблюдателя переменных состояния. Задача условной минимизации функционала (2.8) при ограничениях (2.1), (2.6), (2.7) является частным случаем нелинейной вариационной задачи, решение которой получено в [13] с помощью принципа максимума и инвариантного погружения в виде следующей системы уравнений:
|
|
(4.1) |
|
|
(4.2) |
с начальными условиями:
|
|
(4.3) |
где:
|
|
(4.4) |
Из сравнения
правых частей уравнений (2.6) и (4.1) и формул (1.7), (2.7), (4.4) видно, что
оценку ![]() вектора корректирующих воздействий
вектора корректирующих воздействий ![]() , обращающую в минимум функционал (2.8),
формируют из вектора
, обращающую в минимум функционал (2.8),
формируют из вектора ![]() погрешностей оценивания выходных
сигналов измерительных устройств с помощью алгоритма ПИ-регулирования:
погрешностей оценивания выходных
сигналов измерительных устройств с помощью алгоритма ПИ-регулирования:
|
|
(4.5) |
Алгоритм
оценивания (4.1)-(4.4) получен минимизацией квадратичного функционала (2.8). Из
уравнения Риккати (4.2) и формул (4.3) и (2.7) следует, что матрица Гессе ![]() рассматриваемой задачи оптимизации
положительно определена (либо положительно полуопределена) при любых значениях
параметра регуляризации
рассматриваемой задачи оптимизации
положительно определена (либо положительно полуопределена) при любых значениях
параметра регуляризации ![]() , параметра
, параметра ![]() ПИ-преобразователя (2.7) и элементов
ПИ-преобразователя (2.7) и элементов ![]() диагональной матрицы
диагональной матрицы ![]() нормирующих множителей. Поэтому
динамическая система (4.1)-(4.4) асимптотически устойчива и формирует
единственное решение рассматриваемой задачи условной оптимизации [14]. Но тогда
из условия минимума следует, что переменные
нормирующих множителей. Поэтому
динамическая система (4.1)-(4.4) асимптотически устойчива и формирует
единственное решение рассматриваемой задачи условной оптимизации [14]. Но тогда
из условия минимума следует, что переменные ![]() ,
, ![]() и
и ![]() обращают
в нуль подынтегральное выражение функционала (2.8). После подстановки выражений
(4.5), (2.7) и (4.4) в (2.8) и приведения подобных получим:
обращают
в нуль подынтегральное выражение функционала (2.8). После подстановки выражений
(4.5), (2.7) и (4.4) в (2.8) и приведения подобных получим:
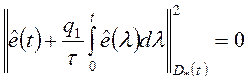 .
.
Так как ![]() ,
, ![]() ,
, ![]() - положительно определенная
диагональная матрица, поэтому:
- положительно определенная
диагональная матрица, поэтому:
|
|
(4.6) |
Из теории
устойчивости Ляпунова известно, что решение линейного дифференциального
уравнения второго порядка с постоянными коэффициентами (4.6) устойчиво при
любых значениях параметров ![]() и
и ![]() ПИ-преобразователя (2.7). Поэтому погрешности
ПИ-преобразователя (2.7). Поэтому погрешности
![]() оценивания выходных сигналов измерительных
устройств с помощью алгоритма (4.1)-(4.4) асимптотически уменьшаются до нуля
при
оценивания выходных сигналов измерительных
устройств с помощью алгоритма (4.1)-(4.4) асимптотически уменьшаются до нуля
при ![]() . Требуемые (желаемые) законы изменения во
времени погрешностей оценивания
. Требуемые (желаемые) законы изменения во
времени погрешностей оценивания ![]() можно обеспечить
выбором числовых значений параметров
можно обеспечить
выбором числовых значений параметров ![]() ,
, ![]() и
и ![]() .
.
5. Синтез формирователя управляющих воздействий. В соответствии с принципом эквивалентности [2], [3] теорией регуляризации А.Н. Тихонова [11] при формировании управляющих воздействий можно использовать регуляризованную модель ОУ (3.8) и регуляризованный функционал МНК (3.9). Но задача минимизации функционала (3.9) при ограничениях (3.8) является частным случаем нелинейной задачи условной оптимизации, решение которой получено в [13] с помощью принципа максимума и инвариантного погружения в виде следующего алгоритма:
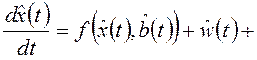
|
|
(5.1) |
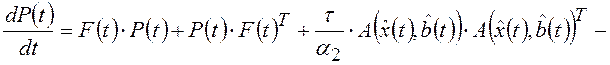
|
|
(5.2) |
где:
|
|
(5.3) |
Из сравнения правых частей уравнений (1.1) и (5.1) и условия несмещенности оценок переменных состояния ОУ следует, что вектор управляющих воздействий, обращающих в минимум функционал (3.9), формирует самонастраивающийся многомерный ПИ-регулятор:
|
|
(5.5) |
с матрицей нестационарных параметров
|
|
(5.6) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.