Разработка и анализ алгоритма настройки параметров ПИ-регуляторов нелинейных систем управления, страница 3

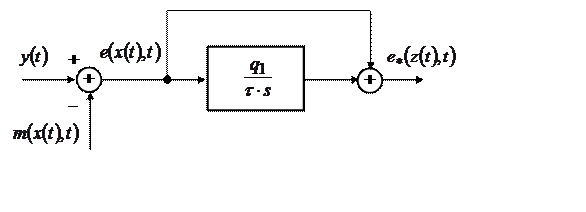
Рис. 1. Структурная схема блока сравнения с ПИ-преобразователем

Блок сравнения с ПИ-преобразователем реализует следующий алгоритм формирования своих выходных сигналов:

где:  - вектор сигналов рассогласования между выходными сигналами ИУ  и их оценками, вычисленными по формулам (1.2), (1.8);   - вектор выходных сигналов ПИ-преобразователя;  - параметр ПИ-преобразователя.

Априорная информация о погрешностях аппроксимации  отсутствует. Поэтому оценки переменных состояния регуляризованной модели ОУ (2.5), (2.6) целесообразно определять минимизацией регуляризованного функционала МНК (РМНК) [11]:

с ограничениями (2.5), где:  - диагональная матрица дисперсий погрешностей задания начальных условий;  - положительно определенная диагональная матрица нормирующих множителей, элементами которой могут быть, например, квадраты пределов абсолютных погрешностей ПИ-преобразователей (2.6);  - параметр регуляризации ().

3. Регуляризация исходной постановки задачи формирования управляющих воздействий. Двухточечные краевые задачи, возникающие при решении задач оптимального управления со свободной правой границей, можно с помощью инвариантного погружения преобразовать в эквивалентные задачи Коши с заданными начальными условиями [12]. В рассматриваемой задаче адаптивного управления можно использовать этот подход, если вместо краевых условий в конечный момент времени управления (1.7) задать ограничения на текущие значения переменных состояния ОУ, гарантирующие выполнение краевых условий (1.7). Будем предполагать, что такая дополнительная априорная информация имеется.

Для части переменных состояния ОУ ограничения на их текущие значения заданы уравнениями (1.6). Поэтому, как это следует из предыдущего анализа, для остальных переменных состояния ОУ необходимо задать ограничения в форме неравенств:

где  ,  - заданные функции своих аргументов, которые принимают в конечный момент времени управления  следующие значения:

При выполнении ограничений (3.1), (3.2) условия (1.7) выполняются гарантированно, поэтому условия (1.7) из числа ограничений можно исключить.

Пусть в результате минимизации функционала (2.7) при ограничении (2.5) определены оценки  вектора переменных состояния ОУ, на который с момента времени  до момента времени  действует вектор управляющих воздействий . Сформируем вектор  вспомогательных функций  по алгоритму:

Из формул (1.6), (3.1)-(3.4) следует, что введенные функции  определяют отклонения текущих значений переменных состояния ОУ от множества допустимых значений, заданных ограничениями (1.6), (1.7), (3.1) и (3.2). Но адаптивная система управления должна учитывать информацию о прошлых и текущих значениях функций  [3]. Поэтому в блок формирования задания регулятору управляющих воздействий предлагается включить многомерный ПИ-преобразователь, который формирует из вектора функций  вектор выходных сигналов  по алгоритму:

где  - параметр ПИ-преобразователя.

Множество допустимых возмущающих воздействий (1.5) зададим с помощью В-сплайны нулевого порядка:

где  - корректирующее входное воздействие, подлежащее определению.

Тогда состояние объекта управления в момент времени   можно определить с помощью следующей регуляризованной модели ОУ:

полученной из уравнения (1.1) заменой возмущающих воздействий  и параметров  объекта управления их оценками  и .

Вектор функций  образован из обобщенных погрешностей управления, поэтому из этих функций сформируем регуляризованный функционал МНК: