














Глава 3. Алгоритмы идентификации параметров модели печи сопротивления и формирования управляющих воздействий
В третьей главе разработана математическая модель в пространстве состояний динамики полезной мощности печи сопротивления и алгоритм идентификации её параметров. Выбрана заданная траектория изменения полезной мощности. Составлен алгоритм формирования управляющего воздействия системы автоматического управления. Обученная модель печи сопротивления используется в контуре обратной связи адаптивной системы автоматического управления полезной мощностью печи сопротивления для настройки оптимальных параметров ПИ-регулятора мощности.
3.1 Самообучаемая математическая модель печи сопротивления в пространстве состояний
Во второй главе изложена
методика определения электрической проводимости печи сопротивления по массиву
измеряемых данных, получаемых от информационно-измерительной системы сбора
электрических параметров. Показано также, что электрическую проводимость печи
сопротивления ![]() следует принять в качестве переменной состояния объекта управления.
следует принять в качестве переменной состояния объекта управления.
Исследованы несколько вариантов математического описания динамики изменения электрической проводимости печи сопротивления:
- дифференциальное уравнение 1-го
порядка с постоянными параметрами: 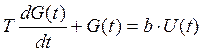 ;
;
- дифференциальное уравнение 2-го
порядка с постоянными параметрами: 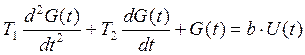 ;
;
- дифференциальное уравнение 1-го
порядка с переменными параметрами: 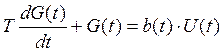 .
.
Идентифицируемым параметром модели
является коэффициент усиления ![]() дифференциального
уравнения. Постоянные времени
дифференциального
уравнения. Постоянные времени ![]() ,
, ![]() оценены с помощью метода наименьших
квадратов [27].
оценены с помощью метода наименьших
квадратов [27].
Оценивание переменного коэффициента
усиления ![]() осуществлялось рекуррентным методом
наименьших квадратов (РМНК) [19, 22, 32, 61] и с помощью B-сплайнов 1-го порядка [37]. Результаты
идентификации приведены на рис. 3.1.
осуществлялось рекуррентным методом
наименьших квадратов (РМНК) [19, 22, 32, 61] и с помощью B-сплайнов 1-го порядка [37]. Результаты
идентификации приведены на рис. 3.1.
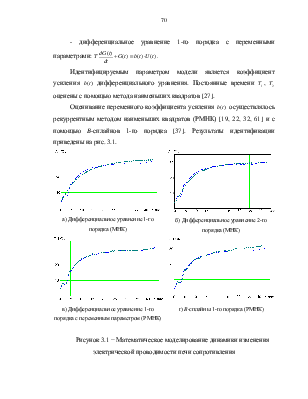
|
а) Дифференциальное уравнение 1-го порядка (МНК) |
б) Дифференциальное уравнение 2-го порядка (МНК) |
|
в) Дифференциальное уравнение 1-го порядка с переменным параметром (РМНК) |
г) B-сплайны 1-го порядка (РМНК) |
Рисунок 3.1 − Математическое моделирование динамики изменения электрической проводимости печи сопротивления
На рисунке 3.2 показано изменение
относительных погрешностей оценивания. Результаты моделирования показали, что
математические модели с постоянным параметром ![]() =const могут лишь усреднённо описать
динамику изменения проводимости печи. Они не позволяют учесть нелинейные
колебания динамики проводимости в течении плавки (особенно в начале плавки),
возникающих из-за физико-химических процессов. Наименьшей погрешностью
оценивания δср = 1.02% обладает модель 1-го порядка
с переменным коэффициентом усиления, оценка которого получена рекуррентным
методом наименьших квадратов.
=const могут лишь усреднённо описать
динамику изменения проводимости печи. Они не позволяют учесть нелинейные
колебания динамики проводимости в течении плавки (особенно в начале плавки),
возникающих из-за физико-химических процессов. Наименьшей погрешностью
оценивания δср = 1.02% обладает модель 1-го порядка
с переменным коэффициентом усиления, оценка которого получена рекуррентным
методом наименьших квадратов.
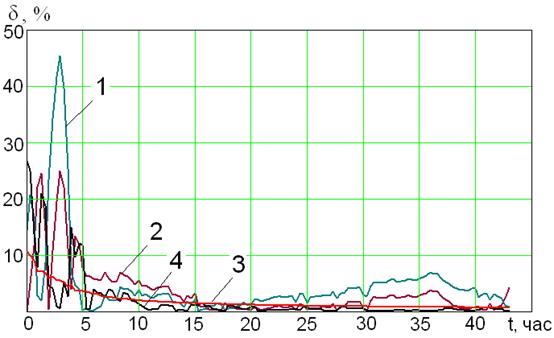
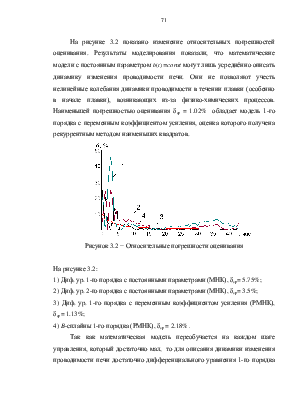
Рисунок 3.2 − Относительные погрешности оценивания
На рисунке 3.2:
1) Диф. ур. 1-го порядка с постоянными параметрами (МНК), δср= 5.75%;
2) Диф. ур. 2-го порядка с постоянными параметрами (МНК), δср= 3.5%;
3) Диф. ур. 1-го порядка с переменным коэффициентом усиления (РМНК), δср= 1.13%;
4) B-сплайны 1-го порядка (РМНК), δср = 2.18% .
Так как математическая модель
переобучается на каждом шаге управления, который достаточно мал, то для
описания динамики изменения проводимости печи достаточно дифференциального
уравнения 1-го порядка с переменным коэффициентом усиления ![]() . Поэтому выбранная
математическая модель печи сопротивления имеет вид:
. Поэтому выбранная
математическая модель печи сопротивления имеет вид:
|
|
(3.1) |
где ![]() =
=![]() − напряжение, подводимое к печи
сопротивления;
− напряжение, подводимое к печи
сопротивления; ![]() −неизвестное возмущающее воздействие; T− постоянная времени динамики изменения электрической проводимости
печи.
−неизвестное возмущающее воздействие; T− постоянная времени динамики изменения электрической проводимости
печи.
Математическая модель может быть записана в матричном виде:
|
|
(3.2) |
где
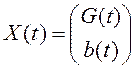 − вектор оценок переменных состояния;
− вектор оценок переменных состояния;
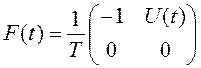 − матрица параметров X(t);
− матрица параметров X(t);
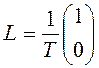 − матрица параметров;
− матрица параметров;
T− постоянная времени процесса изменения проводимости печи, определена по экспериментальным данным 10 плавок карбида кремния, полученным на ОАО «Волжский абразивный завод» и составляет T=200 мин.
3.2 Алгоритм идентификации параметров модели печи сопротивления
В п. 3.1 показано, что в
качестве математической модели динамики изменения электрической проводимости
печи следует использовать модель (3.1), неизвестный параметр ![]() которой рекуррентно оценивается с
помощью РМНК, то есть используется параметрическая идентификация математической
модели в пространстве состояний [36, 54].
которой рекуррентно оценивается с
помощью РМНК, то есть используется параметрическая идентификация математической
модели в пространстве состояний [36, 54].
Для возможности реализации алгоритма идентификации в обратной связи адаптивной системы автоматического управления требуется записать его в рекуррентном виде.
Если математическую
модель печи сопротивления записать в разностном виде ![]() :
:
|
|
(3.3) |
где ![]() − внешние неконтролируемые возмущения,
− внешние неконтролируемые возмущения,
то оценка вектора, полученнная с помощью РМНК будет иметь вид [14, 20]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.