Алгоритмы идентификации параметров модели печи сопротивления и формирования управляющих воздействий, страница 5

с краевыми условиям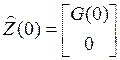и  и .

Из уравнения (3.18) выразим :

Выражение (3.21) подставляют в уравнение (3.19). В итоге уравнения Эйлера-Лагранжа для модели печи сопротивления преобразуются в систему уравнений:

с краевыми условиям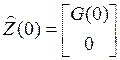и  и .

Таким образом, получена двухточечная краевая задача. Данная задача не имеет аналитического решения. Для численного решения этой задачи применен метод инвариантного погружения [19, 53].

В результате применения метода инвариантного погружения для двухточечной краевой задачи (3.22) и (3.23) был получен следующий алгоритм формирования оптимальных значений переменных состояния системы управления [89]:

где: Q(t) ­­– матрица вспомогательных переменных;

;  .

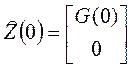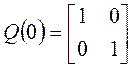В дискретном виде алгоритм будет записан:

Полученное решение обеспечивает минимальную погрешность регулирования при минимальных затратах на управление.

Для нахождения вектора  приравняем уравнение оптимальной траектории  (3.22) и уравнение математической модели объекта управления  (3.12):

Приняв, что , сократим общие множители:

Из выражения (3.27) выразим вектор :

 Нормирующий множитель  можно выбрать равным единице. Так как:

то коэффициенты регулятора могут быть найдены:

Этот алгоритм является асимптотически устойчивым, так как матрица  положительно определённая [19, 34, 53]. При этом он будет сводиться к стационарному решению для любой симметричной неотрицательной определённой матрицы . Т.е. любая ошибка при выборе начального значения  будет стремиться к нулю при  и в конечном счёте будут обеспечиваться оптимальные качественные показатели. При этом скорость сходимости является достаточно высокой [19].

Главным недостатком данного метода является зависимость параметров ПИ-регулятора от  – параметра регуляризации, который выбирается из диапазона [0, 1] опытным путём в процессе управления [72].

3.4 Выводы по главе

По методике, описанной в главе 2, рассчитано изменение полезной мощности печи сопротивления в течении одного плавильного цикла и построен график отношения полезной мощности к полной активной мощности, который представляет собой электрический КПД печной установки. Знание среднего КПД печи может быть полезно для технологов цеха в целях сравнения разных печей между собой по качеству изоляции и выбора наилучших печей, а также для выбора печей, требующих капитального ремонта.

Разработанные в третьей главе рекуррентные алгоритмы идентификации и формирования управляющих воздействий для адаптивной системы автоматического управления полезной мощностью печи сопротивления позволяют идентифицировать параметры самообучаемой математической модели печи сопротивления, находить оптимальные параметры адаптивного ПИ-регулятора в соответствии с обобщённым критерием оптимальности (3.14).

Предполагается, что машинное моделирование процесса автоматического управления полезной мощностью с использованием разработанной математической модели печи позволит еще до экспериментальной плавки сформировать требуемую траекторию плана плавки, реализуемую на конкретном трансформаторе. Это позволит сэкономить время и энергоресурсы предприятия.  Результаты, полученные в третьей главе, опубликованы в работах [8, 14, 16].