Алгоритмы идентификации параметров модели печи сопротивления и формирования управляющих воздействий, страница 4

          В формуле связи полезной мощности  с проводимостью  печи сопротивления присутствует нелинейность, которую можно устранить, считая, что выражение  берётся на момент времени t_k-1, то есть на текущем шаге алгоритма управления считается известным.

Система уравнений (3.11) представлена в матричном виде:

где: ; ;  ;; ; .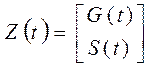

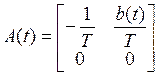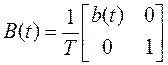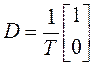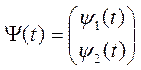В данном представлении модель может быть использована для разработки алгоритма вычисления параметров ПИ-регулятора полезной мощности системы адаптивного управления.

3.3.3 Функционал обобщённой работы для адаптивной системы автоматического управления

Для определения параметров ПИ-регулятора используется функционал обобщённой работы (ФОР) [5]:

где: = T − нормирующий множитель, имеющий размерность времени;  − весовой коэффициент (параметр регуляризации), величину которого выбирают из диапазона , − вектор оценки .

Функционалу обобщенной работы (3.13) даётся следующая физическая трактовка [38]. Числитель первого слагаемого функционала обобщённой работы - это нормированный квадрат сигнала рассогласования между требуемым и измеренным значением полезной мощности в текущий момент времени. Поэтому первое слагаемое определяет величину погрешности управления за период времени  как квадрат сигнала рассогласования. В качестве нормирующего множителя используется допустимая погрешность поддержания плановой мощности .

С другой стороны, квадрат текущего значения амплитуды сигнала пропорционален мощности этого сигнала. Поэтому второе слагаемое определяет величину работы, затраченной за период времени  на формирование управляющего воздействия на объект управления, а именно, вторичного напряжения трансформатора.

Таким образом, функционал обобщенной работы (3.13) представляет собой аддитивную свертку двух показателей качества управления объектом управления, определяющих погрешность управления (первое слагаемое) и затраты энергии на управление (второе слагаемое).

Весовой вклад второго слагаемого в обобщенный показатель качества управления устанавливает параметр , который выбирается экспериментально из диапазона [0,1].

Таким образом, составлен критерий качества управления полезной мощностью печи сопротивления – квадратичный функционал обобщённой работы для адаптивной системы автоматического управления полезной мощностью печи сопротивления для производства карбида кремния. Из формулы (3.13) следует, что оптимальное управление, обращающее в минимум (3.13), обеспечивает минимальный сигнал рассогласования при минимальных затратах на управление активной мощностью.

3.3.4  Алгоритм оптимальной настройки параметров ПИ-регулятора

Требуется найти такие значения 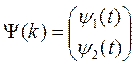, которые обращают в минимум функционал обобщённой работы (3.13) с ограничениями, создаваемыми разностными уравнениями состояния (3.12), т.е. решить задачу условной оптимизации. Для этого с помощью принципа максимума Понтрягина, выполнена следующая последовательность действий.

С помощью вектора неопределенных множителей Лагранжа преобразуем задачу условной оптимизации функционала обобщённой работы (3.13) с ограничениями (3.12) в задачу безусловной оптимизации функции Гамильтона ():

где      – вектор неопределённых множителей Лагранжа, подлежащих определению.

Требуется минимизировать функцию Гамильтона (3.14) по ,. Для этого используют необходимые и достаточные условия экстремума (уравнения Эйлера-Лагранжа):

с краевыми условиям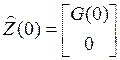и  и .

Уравнения Эйлера-Лагранжа для модели печи сопротивления примут вид: