Алгоритмы идентификации параметров модели печи сопротивления и формирования управляющих воздействий, страница 3

Из рис.3.5 видно, что почти для всех плавок электрический КПД печи повышается к концу плавильного цикла. Это можно объяснить тем, что сопротивление печи постепенно падает (проводимость растёт) вследствие образования кристаллов SiC и роста сечения керна, а проводимость металлического каркаса печи после разогрева остаётся примерно постоянной. В результате, шихта начинает забирать больше тока, чем каркас печи, что увеличивает электрический КПД печной установки.

Стоит отметить, что совпадение динамики КПД с динамикой роста активной мощности печи в течении плавильной кампании (рис.3.5) характерно для постоянного плана плавки. На рис. 3.6, 3.7 приведены графики электрического КПД и мощности для опытной плавки со ступенчатым планом. Плавка проведена на трансформаторе №22 с 49 ступенями напряжения. Длительность плавки составила 40 часов. План плавки задан по выбору электроэнергии: при 0-30 МВт/ч  P_пл1=4000 кВт/ч; при 30-70 МВт/ч P_пл2=2800 кВт/ч; при 70-120 МВт/ч P_пл3=2600 кВт/ч.

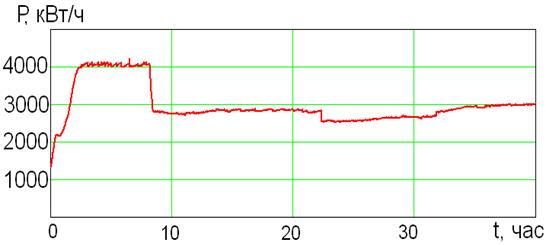
Рис. 3.6 − Изменение активной мощности опытной плавки со ступенчатым планом

Рис. 3.7 − Изменение электрического КПД опытной плавки со ступенчатым планом

Из рисунков 3.6, 3.7 видно, что КПД быстро растёт в начале плавки, так же как и активная мощность. При резком уменьшении вводимой мощности на 1.2 МВт/ч (через 8 часов после начала плавки) КПД сохраняется практически на том же уровне (93%). Средний уровень КПД за время плавильной кампании выше чем у плавок с постоянным планом на 3-4%,  а значит эту плавку можно считать более эффективной по количеству фактически потреблённой электроэнергии печью.

Таким образом из рис. 3.5 видно, что при поддержании измеряемой активной мощности на заданном уровне, полезная мощность на участке регулирования составляет 85-95% от полной активной мощности. Поэтому заданная траектория изменения полезной мощности может быть принята линейной на уровне 2500 - 2600 кВт/ч, или ступенчатой с произвольным заданием (в диапазоне 1000-4000 кВт/ч). Для выбора наилучшего значения плана плавки требуется накопить соответсвтующую статистику.

Возможен вариант добавления в систему управления блока пересчёта плана плавки, который вычисляет плановую полезную мощность по заданному плану для активной мощности и текущему значению КПД печи.

3.3.2 Математическая модель замкнутой системы управления с ПИ-регулятором

Для управления выбран ПИ-регулятор, обеспечивающий нулевую статическую погрешность для линейных объектов. ПИ-регулятор вырабатывает управляющее воздействие согласно математической модели:

где сигнал рассогласования  определяется как разность между требуемым сигналом задания Y_ТР  и текущим выходом объекта управления Y:

Если обозначить:

то  можно записать:

 Обозначим вход «И» части регулятора как . Следовательно  . Тогда дифференциальное уравнение для  запишется:

Структурная схема ПИ-регулятора:

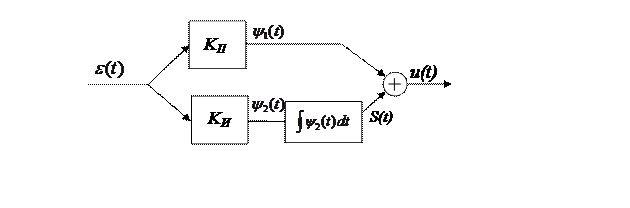
Таким образом, если найти вспомогательные переменные , то можно вычислить параметры регулятора K_П, K_И.

Объединив математическую модель объекта управления (3.1), уравнения для вычисления полезной мощности (2.9), электрической проводимости (2.11) и ПИ-регулятора можно записать математическую модель объекта управления с ПИ-регулятором в пространстве состояний:

где:  − допустимая погрешность поддержания плановой мощности; ,  − переменные состояния регулятора;  − выход И-части регулятора.