Лекция 14
Коррекция систем автоматического управления
План:
1. Способы улучшения точности динамической системы
2. Инвариантные системы
3. Корректирующие устройства систем управления
4. Частотный метод синтеза систем управления
Как было доказано в предыдущей лекции, величина установившейся ошибки напрямую зависит от величины или скорости изменения входного воздействия и обратно зависит от общего коэффициента передачи по контуру. Отсюда вытекает простейший путь повышения точности – увеличение коэффициента передачи К, так как
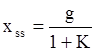 .
.
Однако, с ростом К часто могут быть нарушены условия устойчивости.
Основной путь для уменьшения установившейся ошибки – это повышение порядка астатизма. Используя этот метод, мы делаем равными нулю первые в ряду коэффициенты ошибок в системе. Например, для системы с астатизмом третьего порядка c0=c1=c2=0. Повышение порядка астатизма наиболее просто производится за счет последовательно включенных в контур интеграторов. Рассмотрим пример из предыдущей лекции:
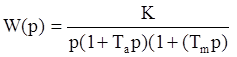 - 1-й порядок астатизма.
- 1-й порядок астатизма.
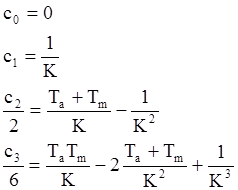
Введем интегрирующее звено в систему (рис.1).
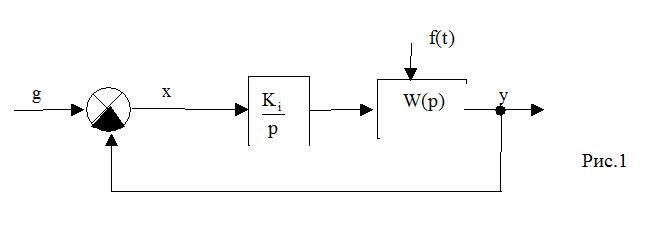
Передаточная функция скорректированной разомкнутой системы имеет вид
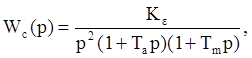 где
где ![]() - добротность системы по ускорению.
- добротность системы по ускорению.
Тогда передаточная функция замкнутой системы по ошибке:
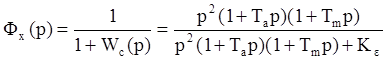
Разложив ее в ряд, получим коэффициенты ошибок:
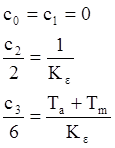
Так как c1=0 , то установившаяся ошибка для воздействия с постоянной скоростью будет равна нулю.
Повышение порядка астатизма на единицу
ведет к увеличению фазового запаздывания ситемы на величину ![]() . Следовательно, это также може нарушить
устойчивость системы. Фазочастотная характеристика рассмотренной системы
(рис.1) будет начинаться на уровне (
. Следовательно, это также може нарушить
устойчивость системы. Фазочастотная характеристика рассмотренной системы
(рис.1) будет начинаться на уровне (![]() ) – для
) – для ![]() ; и будет продолженав области фазовых
запаздываний
; и будет продолженав области фазовых
запаздываний ![]() с ростом частоты. Эта система не может
быть устойчивой для любого значения коэффициента усиления
с ростом частоты. Эта система не может
быть устойчивой для любого значения коэффициента усиления ![]() и нуждается в дополнительной коррекции.
и нуждается в дополнительной коррекции.
Другой метод повышения порядка астатизма - введение изодромного звена в контур управления (рис.2)
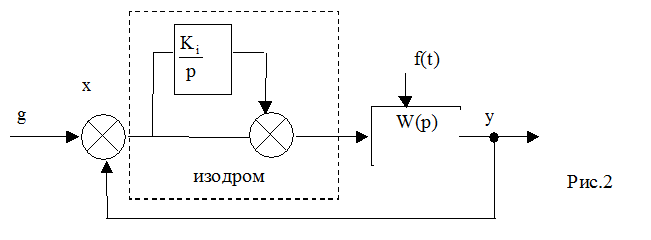
Передаточная функция изодрома имеет вид
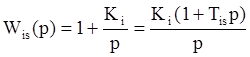
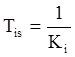
Для рассмотренного примера скорректированная передаточная функция разомкнутой системы будет иметь вид:
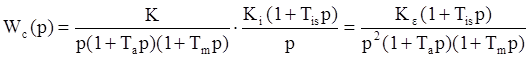
Анализируя характеристическое уравнение, можно заключить, что для достаточно большой величинв Tis получим условие устойчивости, эквивалентное условию устойчивости исходной системы:
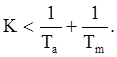
Для увеличения порядка астатизма более, чем на единицу следует включать в контур управления требуемое количество последовательных изодромных звеньев.
Для улучшения точности системы и для увеличения запасов устойчивости можно использовать управление с введением производной от ошибки (рис. 3). Такая система чувствительна не только к величине ошибки, но и к скорости ее изменения. Поэтому время реакции системы уменьшается.
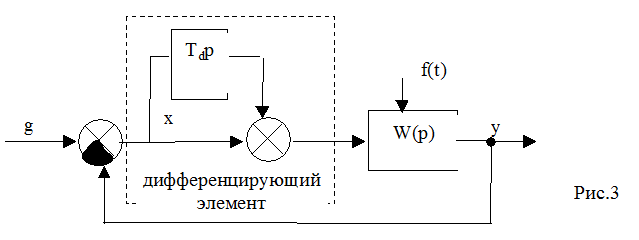
Передаточная
функция дифференцирующего элемента ![]() . В нашем примере с
подобной коррекцией передаточная замкнутой системы по ошибке будет получена как
. В нашем примере с
подобной коррекцией передаточная замкнутой системы по ошибке будет получена как
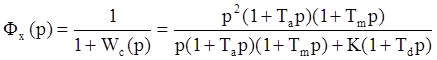
Коэффициенты ошибок равны:
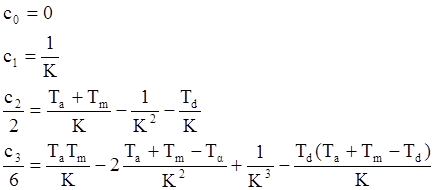
Из этих формул можно найти величину Td при которой можно обеспечить c2=0 или c3=0. Используя два последовательных корректирующих устройства с дифференцирующими элементами, можно обеспечить одновременное выполнение условий c2=0 и c3=0 .
Для производственных систем регулирования широко распространено использование дополнительных звеньев для улучшения качества управления. Различные типы регуляторов часто называют в соответствии с выполняемыми ими функциями:
- P (proportional) пропорциональный регулятор;
- PI (proportional – integrating) пропорционально-интегрирующий регулятор;
- PD (proportional – differentiating) пропорционально-дифференцирующий регулятор;
- PID (proportional – integrating – differentiating) пропорционально—интегрирующе-дифференцирующий регулятор.
Автоматическая система будет называться инвариантной по отношению к какому-либо сигналу, если по завершению переходного процесса величина ошибки не зависит от вида взодного сигнала. Так система с астатизмом первого порядка будет инвариантноа по отношеню к постоянному входному сигналу.
Следящая система будет называться абсолютно
инвариантной к управляющему воздействию, еслиможно свести передаточную функцию
по этому воздействию к некоторому масштабирующему коэффициенту передачи К.
Следовательно, для абсолютно инвариантной системы можно записать ![]()
Основной метод синтеза интвариантных систем – это применение комбинированного управления. Применяя этот метод, вводят помимо управления по ошибке ( по отклонению) и управление по входному воздействию g (рис.4).
Если в этой системе Wg(p)=0, то выходная величина y связана со входным сигналом через выражение:
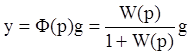
Если же ввести связь Wg(p)≠0, то
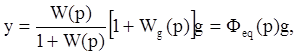
где ![]() -
эквивалентная передаточная функция замкнутой системы:
-
эквивалентная передаточная функция замкнутой системы:
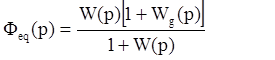 (1)
(1)
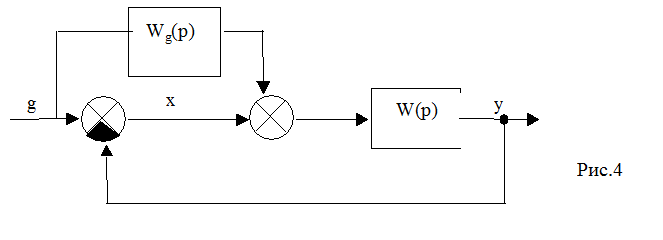
Поскольку знаменатель у этой передаточной функции такой же, как и у нескорректированной системы, то измененная система имеет такое же характеристическое уравнение. Следовательно, введение дополнительной цепи управления не нарушает устойчивости системы и сохраняет основные характеристики переходного процесса прежними.
Из выражения (1) можно получить вид эквивалентной передаточной функции системы по ошибке:
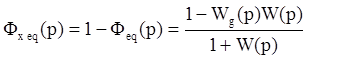 (2)
(2)
и эквивалентную передаточную функцию разомкнутой системы:
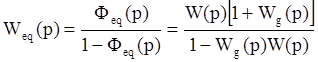
Из выражения (2) видно, что для полной
инвариантности системы необходимо обеспечить выполнение условия 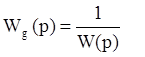 .( чтобы выполнялось условие Фeq x=0)/
.( чтобы выполнялось условие Фeq x=0)/
Разложив последнее выражение в ряд, получим:
![]() (3)
(3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.