Величина a0 для астатических систем и для большинства статических систем равна нулю. То есть для получения абсолютно инвариантной системы следует применить комбинированное управление по первой проихзводной и по производным более высокого порядка от входного сигнала. Поскольку практическая реализация передаточной функции корректирующей цепи (3) крайне затруднительна (обычно можно ввести только первую производную), то применение комбинированного управления обеспечивает только частичную инвариантность системы.
Подобно комбинированному управлению по входному синалу можно ввести и комбинированное управление по возмущающему воздействию.
Таким образом, видно, что применяемые для повышения качества систем регулирования повышение порядка астатизма и повышение общего коэффициента передачи разомкнутого контура обычно ведут у потере устойчивости и для обеспечения необходимых запасов устойчивости необходимо включать специальные корректирующие устройства (корректирующие звенья). Их можно разделить на последовательные, параллельные и устройства, образующие местную обратную связь.
Последовательная коррекция наиболее удобна для синтеза систем в частотной области, так как частотные характеристики таких корректирующих устройств можно непосредственно умножать (а в логарифмическом масштабе – складывать) с частотными характеристиками нескорректированной системы.
Рассмотрим наиболее распространенные типы последовательных корректирующих устройств, которые можно реализовать посредством эквивалентных схем пассивных четырехполюсников электрических R-C – цепей.
1) Дифференцирующее звено с передаточной функцией:
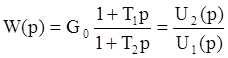(4)
Его частотные характеристики имеют вид:
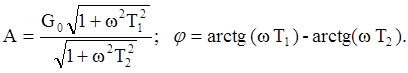
Эквивалентная схема звена представлена на рис.5a, ЛАФЧХ – на рис.5b.
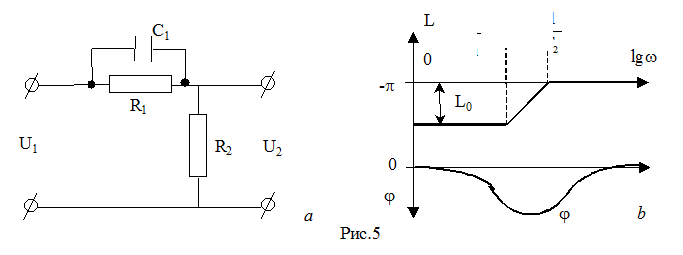
Параметры эквивалентной схемы вычисляются таким образом:
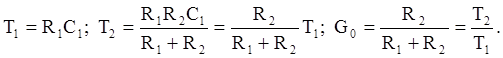
Это наиболее простое корректирующее звено для сдвига фазовой характеристики в положительную область (повышение устойчивости). Действие звена определяется величиной соотношения G0 связанной с реальными параметрами R1 и R2.
2) Интегрирующее звено с передаточной функцией:
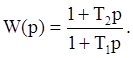(5)
Частотные характеристики звена запишутся в виде:
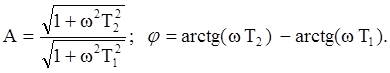
ЛАФЧХ звена и его эквивалентная схема представлены на рис.6.
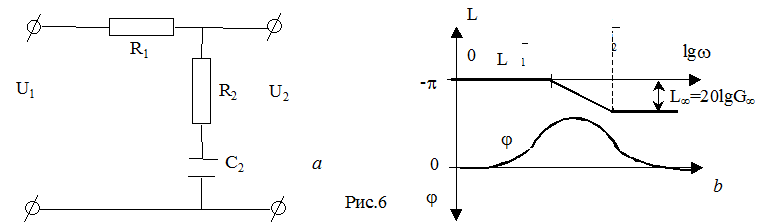
Параметры схемы вычисляются следующим образом
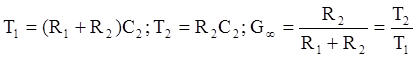
Обычно это звено используется для снижения амплитудной характеристики на высоких частотах, что улучшает защищенность системы от помех, а также может служить для уменьшения частоты среза ωc системы.
3) Интегро-дифференцирующее звено (рис.7).
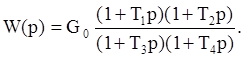
Его частотные характеристики имеют вид:
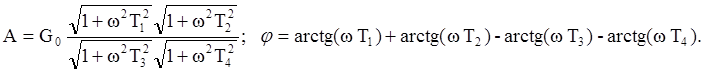
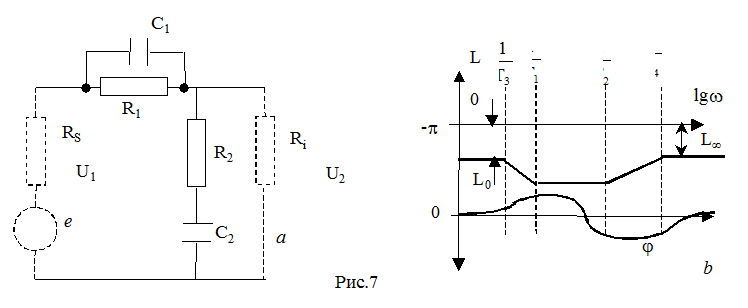
Параметры эквивалентной схемы получаются как:
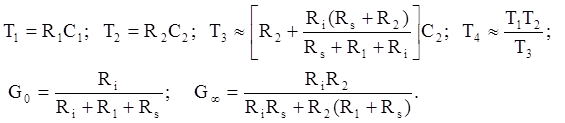
Такое звено подавляет усиление в определенном диапазоне частот.
Рассмотрим передаточную функцию разомкнутой системы с астатизмом первого порядка
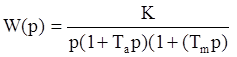
В этой системе коэффициент добротности по скорости ограничен условием
,
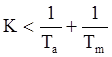при невыполнении которого теряется устойчивость. Дополним передаточную функцию разомкнутой системы последовательным дифференцирующим фильтром.
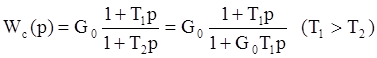
В итоге передаточная функция разомкнутой системы получит вид:
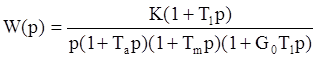
Положим для Wc(p) условие T1=Tm, тогда
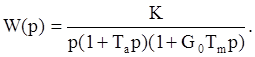
Составим характеристическое уравнение 1+W(p)=0:
,
которое даст нам условие устойчивости
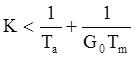
Таким образом, варьируя величину G0 можно получать устойчивую систему в широком диапазоне общего коэффициента передачи системы по скорости K.
Если мы располагаем некоторой логарифмической частотной характеристикой системы, то легко геометрически построить логарифмическую частотную характеристику корректирующего устройства как разность между располагаемой и желаемой частотными характеристиками. Используя далее связь между параметрами корректирующих цепей и расположением их частотных характеристик, можно найти параметры устройств коррекции, обеспечивающих необходимые качества системы.
Покажем здесь основные требования, предъявляемые при построении желаемой ЛАФЧХ.
1) Низкочастотная область.
Эта часть частотной характеристики должна обеспечить заданную точность системы в установившемся режиме.
Если полезный входной сигнал имеет вид:
То для того, чтобы величина ошибки по амплитуде не превысила xm необходимо обеспечить, чтобы низкочастотная ветвь ЛАЧХ проходила бы не ниже точки AK с координатами
.
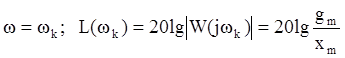Используя условие минимизации установившейся ошибки для входных воздействий с постоянной скоростью и постоянным ускорением получаем запретную зону, в которую не должна заходить низкочастотная часть ЛАЧХ разомкнутой системы (рис.8).
2) Среднечастотная область.
Для следящих систем рекомендуется ЛАЧХ, проходящая в среднечастотной области с наклоном (-20dB/dec) в районе частоты среза ωc.
Для того, чтобы обеспечить желаемый коэффициент
колебательности системы M и соответствующие запасы устойчивости, следует
изобразить вокруг точки пересечения ЛАЧХ с осью 0 dB (частота ωc
(L(ωc)=0) (рис.8.4).) окружность, которая будет являться запрещенной
зоной для фазовой частотной характеристики, если ось 0 dB совпадает с осью
(-180о). Если взять за базу точку 
, то
можно получить значения постоянных времени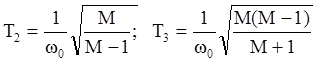 
,которые определяют границы среднечастотной области и, соответственно, изломы асимптотической ЛАЧХ.
3) Высокочастотная область.
Для зоны частот 
необходимо обеспечить
максимальный отрицательный наклон ЛАЧХ, чтобы подавить помехи, которые обычно
имеют характер высокочастотных шумов. Однако для частоты излома асимптотической
ЛАЧХ q0 следует принять во внимание реальную форму
амплитудно-частотной характеристики, которая может иметь резонансный пик. Чтобы
не произошло потери устойчивости, следует обеспечить некоторый запас по
амплитуде на этой частоте:
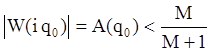
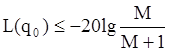
Это влечет за собой введение дополнительной запретной зоны для амплитудно-частотной характеристики (рис.8).
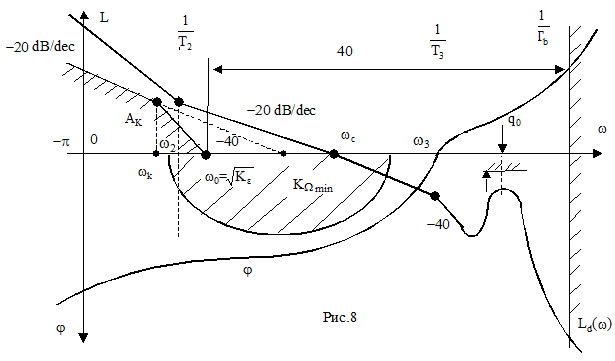
Таким образом, получена желаемая амплитудно-частотная характеристика системы Ld(ω), которая используется при построении последовательных корректирующих устройств.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.