Методы решения дифференциальных уравнений систем управления. Операторные методы. Преобразование Лапласа

Лекция 6

Методы решения дифференциальных уравнений систем управления. Операторные методы.

 Преобразование Лапласа

План:

1.  Численные методы решения дифференциальных уравнений

2.  Аналитические методы решения дифференциальных уравнений

3.  Преобразование Лапласа и его свойства

Продолжая изучать свойства следящей системы, рассмотренной в предыдущих лекциях, рассмотрим, как можно решить дифференциальные уравнения системы, записанные в форме (1). Эта форма носит название нормальной формы Коши. В левой части уравнений мы имеем производные первого порядка по времени от фазовых переменных, правая часть уравнений выражает их через  независимые фазовые переменные и внешние воздействия.

Для решения системы мы должны знать начальные условия по всем фазовым переменным и их скоростям, выражения для внешних воздействий.

Наиболее распространенный путь решения дифференциальных уравнений – это их численное интегрирование. Наиболее простым и распространенным методом численного интегрирования является метод Эйлера. Для его использования необходимо задать элементарный шаг по времени h. Затем для каждой фазовой переменной записывается выражение,

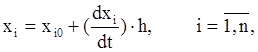
где x_i0-начальное значение переменной  x_i  (x_i0=x_i(t=0)).

В качестве производных  мы должны подставить правые части дифференциальных уравнений в нормальной форме, вычисленные  для данных начальных условий.

Для нашего примера следящей системы, рассмотренной выше фазовые переменные будут вычисляться в соответствии с системой уравнений :

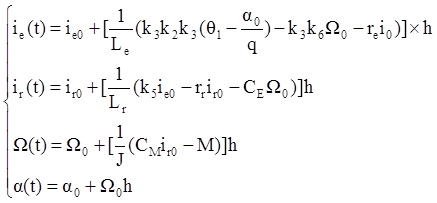
В соответствии с этой системой мы должны вычислить величины всех фазовых переменных для момента времени  t=0+h. Затем мы принимаем  x_i0=x_i и повторяем все вычисления для новых значений фазовых переменных для моментов времени  t=2h, далее для  t=3h и т.д. Так мы можем построить функции x_i(t); (t=h, 2h, 3h…) в качестве решения системы . Чем меньше величина шага h, тем выше точность вычислений. Другие более сложные и точные методы численного интегрирования (например Рунге-Кутта) имеют специальные средства устранения накапливающейся ошибки

Основным преимуществом численных методов является то, что они используются для анализа не только линейных, но и нелинейных систем управления. Однако их главный недостаток – большие затраты вычислительных ресурсов.. Поэтому для линейных систем предпочтительнее использовать аналитические выражения для решений дифференциальных уравнений.

В соответствии с классическим методом решения дифференциальных уравнений необходимо с учетом формы уравнения составить его характеристическое уравнение, при решении которого определяется вид функции , являющейся  решением. Затем для подобранной формы по начальным условиям определяются константы – параметры.

Пусть имеется дифференциальное уравнение в свернутой форме ((3) из предыдущей лекции).

D(p)x(t)=Q(p)g(t)+N(p)f(t),              (1)

где D(p), Q(p), N(p) – полиномы относительно обобщенного оператора дифференцирования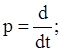  

x(t) – переменная состояния системы;

 g(t) и  f(t) – управляющее и возмущающее воздействия.

Тогда решение дифференциального уравнения (1) может быть описано формулой:

x(t)=x₀(t)+x_p(t),

где x₀(t) – общее решение однородного уравнения D(p) x(t)=0, которое имеет форму

  в которой C₁..C_n – константы, определяемые начальными условиями;

 p₁..p_n – корни характеристического уравнения D(p)=0.

Частное решение x_p(t) определяется правой частью уравнения (1) и соответствует некоторому установившемуся процессу при функционировании системы.  Частные решения для различных управляющих и возмущающих воздействий могут вычисляться независимо, а затем быть просуммированы (об этом подробнее будет указано ниже).

Исследование связей между входным и выходным  сигналами значительно облегчается, если использовать изображения  сигналов в  преобразованиях Фурье и Лапласа.

Пусть имеется сигнал .

Преобразование Лапласа этой функции времени будет иметь  свойства, перечисленные в таблице 1.

Таблица 1        Свойства преобразования Лапласа

Сигнал
Изображение (Прямое преобразование)
Комплексная переменная  ( оператор Лапласа)
Ядро (решение)
Условие существования
Обратное  преобразование
Свертка

Преобразование Лапласа позволяет решить дифференциальные уравнения системы более  экономичным способом, чем с применением обычных приемов.

Для этого используют таблицу стандартных изображений функций по Лапласу (при нулевых начальных условиях ): (Таблица 2).

Таблица 2        Преобразование Лапласа стандартных функций

F(t)
1 (t)	1/p
	A/p

Для решения дифференциального уравнения, необходимо применить преобразование Лапласа к его правой и левой  частям. Затем  находят изображение выходной величины в  преобразовании по Лапласу. После разложения этого изображения на  элементарные слагаемые в соответствии  с Таблицей 2 мы легко можем найти оригинал функции изменения выходной величины (с нулевыми начальными условиями). Если  начальные значения переменных отличны от нуля,  то  используют следующую теорему:

Теорема 1:

Если функция f(t) и первая производная  являются оригиналами и F (p) - изображение по Лапласу, то

L [] = p F (p) - f (0 +),

Где f (0 +) = .

Для производных более высокого порядка мы можем найти изображение в соответствии с формулой:

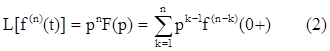
Еще одна важная теорема о конечном значении в преобразовании Лапласа используется для оценки установившихся значений сигналов:

Теорема 2:

Если функция f (t) и ее первая производная  являются оригиналами и F (p) - изображение по Лапласу, и p F (p) - аналитическая функция, то

Рассмотрим пример:

Требуется найти решение дифференциального уравнения  с начальными условиями x(0)=0; .

Решение:

Пусть  . Выполним  преобразование Лапласа с учетом выражения (2):

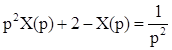
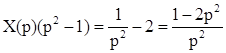
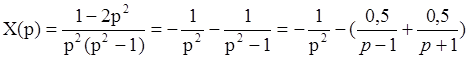
В соответствии с таблицей 2:

x(t)=-(t-0.5exp(t)+0,5exp(t))1(t)