Лекция 12
Устойчивость линейных динамических систем
План:
1. Определение устойчивости динамической системы
2. Алгебраические критерии устойчивости
3. Частотные критерии устойчивости
4. Анализ устойчивости с помощью логарифмических частотных характеристик
Когда мы говорим об устойчивости системы управления, то мы имеем в виду либо устойчивость состояния покоя (равновесия) , либо устойчивость установившегося периодического движения. В теории управления обычно рассматривают устойчивость невозмущенного движения.
Дифференциальное уравнение системы можно записать относительно отклонения (возмущения):
![]() (1)
(1)
Пусть причиной возмущения является начальное
отклонение из положения равновесия ![]() , которое лежит внутри
ближайшей области около положения равновесия. Пусть размер этой области
равен e. Если это отклонение не приводит к выходу
возмущенного движения
, которое лежит внутри
ближайшей области около положения равновесия. Пусть размер этой области
равен e. Если это отклонение не приводит к выходу
возмущенного движения ![]() из области
из области ![]() , то такая система будет устойчивой по
А.М. Ляпунову.
, то такая система будет устойчивой по
А.М. Ляпунову.
![]() , (2)
, (2)
то говорят об асимптотической устойчивости состояния равновесия системы.
Решение уравнения (1) для случая линейной системы будет иметь вид:
![]()
где![]() - корни
характеристического уравнения системы (действительные или комплексные).
- корни
характеристического уравнения системы (действительные или комплексные).
Таким образом, вид переходного процесса в системе будет зависеть от распределения корней характеристического уравнения.
Если все корни характеристического уравнения имеют отрицательные действительные части, то выполняется условие (2) и переходный процесс носит затухающий характер (рис 1,a). Если хотя бы один из корней имеет положительную действительную часть, то переходный процесс будет неограниченно расходящимся (рис 1,b), и такая система не будет устойчивой.
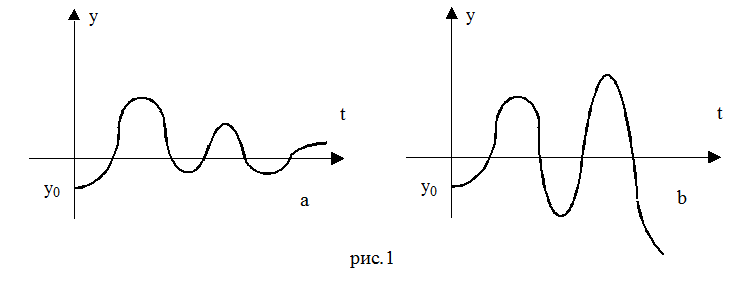
Таким образом, можно сказать, что необходимым и достаточным условием устойчивости линейной системе является отсутствие положительных корней характеристического уравнения.
Если характеристическое уравнение системы имеет нулевой корень l =0, то она находится на апериодической границе устойчивости (состояние безразличного равновесия). (рис.2,a). Если в системе имеется пара чисто мнимых корней с нулевой действительной частью, то система находится на колебательной границе устойчивости (рис.2,b):
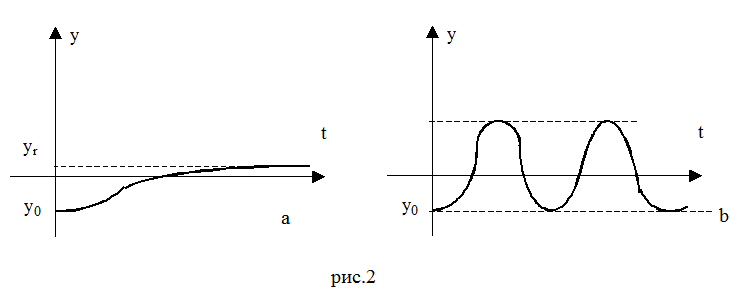
Необходимым и достаточным условием устойчивости линейной динамической системы является отсутствие корней характеристического уравнения с положительными действительными частями. Чтобы установить справедливость этого условия нет необходимости вычислять все корни и даже составлять характеристическое уравнение. Для этого применяются критерии устойчивости, которые разделяются на алгебраические и частотные.
В качестве необходимого алгебраического условия устойчивости выступает то, что все коэффициенты характеристического полинома должны быть положительными (быть одного знака). Для нахождения достаточного условия требуется дополнительный анализ коэффициентов.
Критерий Гурвица. Этот критерий позволяет определить знак всех корней характеристического уравнения без их вычисления.
Пусть характеристический полином имеет вид:
![]()
Составим определитель Гурвица в виде:
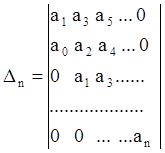
и запишем его диагональные миноры
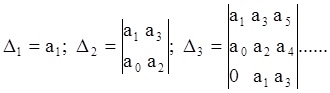
Последний определитель можно выразить через предпоследний:
![]()
По критерию Гурвица необходимым и достаточным условием устойчивости системы является выполнение следующей системы неравенств:
![]()
Используя этот критерий легко установить, что для систем первого и второго порядка необходимое условие является и достаточным:
![]()
Для системы третьего порядка это условие приобретает вид:
![]()
(Условие устойчивости Вышнеградского).
Критерий Михайлова. Все частотные критерии
устойчивости базируются на преобразовании Фурье (в передаточной функции
выполняем подстановку ![]() ) и принципе аргумента, сущность
которого заключается в следующем.
) и принципе аргумента, сущность
которого заключается в следующем.
Характеристическое уравнение системы можно записать в следующем виде:
![]()
Выполнив подстановку в соответствии с
преобразованием Фурье ![]() , получим характеристический
вектор:
, получим характеристический
вектор:
![]()
![]() это
комплексное произведение элементарных векторов (рис.3,a)
это
комплексное произведение элементарных векторов (рис.3,a)
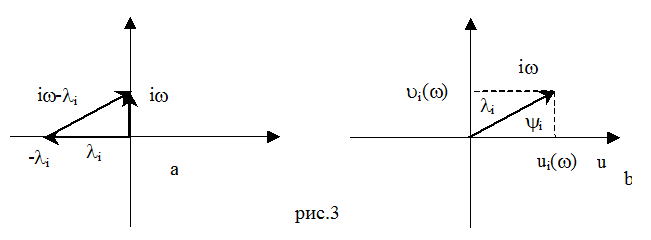
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.