Лекция 3
Типы управляющих и возмущающих воздействий
План
1. Примеры управляющих и возмущающих воздействий
2. Описание сигналов с помощью единичной ступенчатой и δ-функции.
3. Непрерывные и дискретные сигналы
4. Детерминированные и случайные сигналы
При рассмотрении любой автоматической системы всегда можно выделить сигналы (воздействия)влияющие на состояние системы.
Рассмотрим систему стабилизации температуры некоторого объекта (рис.1).
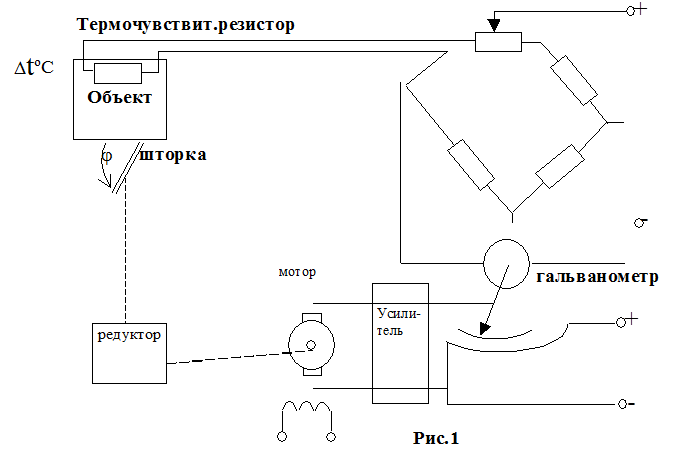
В этой системе обязательно следует принять во внимание следующие два воздействия. Первое из них - это возмущающее воздействие – изменение температуры объекта. Второе – это управляющее воздействие – смещение движка задающего потенциометра. Оно задает для системы входную величину, к которой должна стремиться выходная величина - температура объекта. По типу задающих воздействий системы как раз и делятся на системы стабилизации, следящие системы и системы программного управления.
Рассмотрим более подробно два случая.
1. Постоянное управляющее воздействие. В такой системе каждое положение движка потенциометра соответствует определенной температуре объекта. Когда мы включаем систему, или когда мы переместили движок из одного положения в другое достаточно быстро, мы получаем скачок управляющего воздействия (рис.2a).
2. Программное управления (рис.2b). Температура должна меняться в соответствии с заданной функцией.
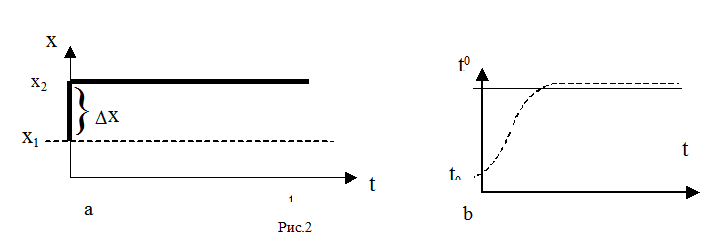
В первом случае мы всегда имеем дело со ступенчатой функцией. Температура измеряется в градусах , положение потенциометра – в метрах. При описании систем управления чаще всего используют безразмерные единицы. Поэтому для математического описания таких процессов вводится стандартная безразмерная функция. Она называется единичной ступенчатой функцией 1(t).
Эта функция может быть изображена графически (рис.3):

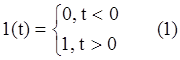
Посредством единичной ступенчатой функции мы можем изобразить скачок управляющего воздействия (рис 2a) с помощью следующей формулы:
![]()
Если
начальное значение переменной x=0, то ![]()
Функция (1) очень удобна, если скачок той или иной величины происходит в начальный момент времени (при включении системы). Но этот начальный момент ( при t=0) не всегда совпадает с временем того или иного скачка управляющего воздействия и почти никогда не совпадает со скачком возмущающего воздействия. Поэтому в теории управления широко используется также смещенная единичная ступенчатая функция (функция 1(t) с запаздыванием)(рис.4):
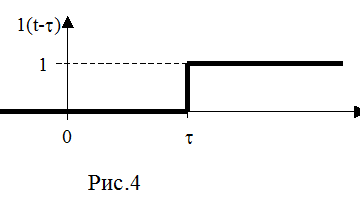
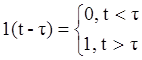
Величина t называется чистым (транспортным) запаздыванием.
Таким образом мы можем дать математическую модель практически любого процесса в системе управления через комбинацию описывающих функций и единичных ступенчатых функций (со смещением или без). Некоторые сигналы в автоматических системах как внезапно появляются, так и внезапно исчезают.(см. рис.5)
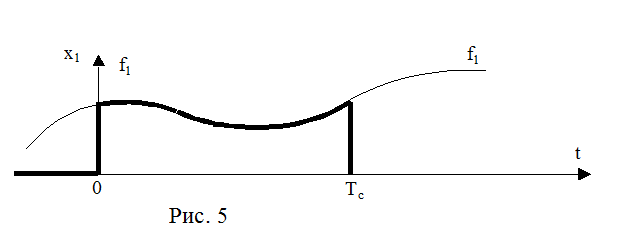
здесь 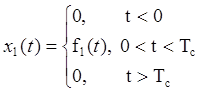
таким образом, мы можем записать:
![]()
Все сигналы рассмотренные выше , мы считали непрерывными. Но если время Tc (рис.5) очень мало по сравнению со временем всего процесса, мы можем говорить об импульсе сигнала. Такой импульс может быть описан с помощью интеграла
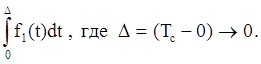
Время импульса можно считать мгновенным. Будем считать, что импульс возникает в середине интервала D l. Обычно импульсы следуют друг за другом через равные периоды времени T. Интервал D должен удовлетворять условию D<T. Если D<<T, мы имеем последовательность мгновенных импульсов (рис..6):
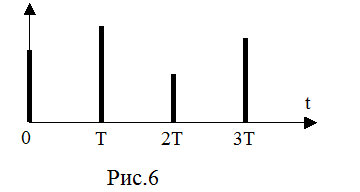
Если D=T получаем кусочно-непрерывный сигнал (рис.7):
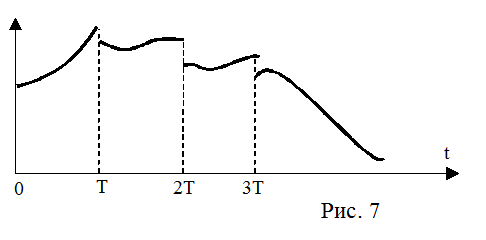
Каждый импульс в серии на рис.6 можно описать как прямоугольник с бесконечно большой высотой и бесконечно малой шириной (длительностью). Чтобы записать такую функцию в виде формулы, используется импульсная функция Дирака (d-функция):
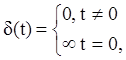
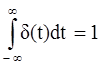
Легко видеть, что d - функция является первой производной от единичной ступенчатой функции:
![]() ,
,
потому что скорость изменения функции 1(t), изменяющейся в момент времени t=0 скачком, неограниченно возрастает в момент скачка и равна нулю в любой другой момент времени (t¹0) для 1(t), которая при этом постоянна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.