Типы управляющих и возмущающих воздействий, страница 2

Аналогично с единичной ступенчатой функцией, для  d-функции можно ввести запаздывание 

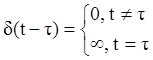
Если имеются периодические импульсы (как на рис.6), то можно предположить, что амплитуда импульса (A) в течение времени его действия не меняется и  импульс, приходящийся на момент t₀ можно описать с помощью выражения Ad(t-t₀) D.

Если t₀=nT (n=0,1,2…) , то

F(t)=A[d(t)+ d(t-t)+d(t-2T)+…] D

Далее, если величина A меняется  от импульса к импульсу  согласно зависимости A = f(t),.

То импульсный сигнал может быть описан через формулу

F(t)=f(t)[d(t)+ d(t-t)+…] D

Если D<<T, то имеем дискретную форму функции:

F(t)=f[nT]  ,(n=0,1,2…),

которую называют также решетчатой функцией  f[n].

Аналогично непрерывной единичной ступенчатой функции можно ввести решетчатую единичную ступенчатую функцию и представить дискретный сигнал как произведение единичной ступенчатой решетчатой функции и описывающей функции:

x[n]=f(t)1[n]

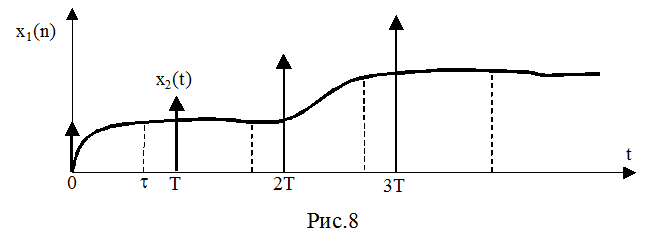
Часто решетчатая функция является результатом некоторого другого воздействия на систему и дискретизации внутри нее. Таким образом, время дискретизации сигнала на выходе объекта x₂(t) будет смещено относительно времени дискретизации входного сигнала x₁(t) на некоторую постоянную величину t.  В этом случае имеем смещенную решетчатую функцию с относительным временем запаздывания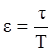 

Изменяя величину e, можно получать реакцию непрерывного объекта на дискретный сигнал в любой момент времени (рис.8).

Таким образом мы изучили два типа воздействий (которые могут быть управляющими или возмущающими) – дискретные и непрерывные. Оба они предполагаются детерминированными. Это означает,  что описывающие функции f(t) или f[n]  этих воздействий  всегда можно выразить через точные формулы. Типы описывающих функций могут быть совершенно различными – гармонические,  линейно меняющиеся, постоянные,  экспоненциальные и др. Системы , в которых все воздействия (сигналы) являются детерминированными,  также называются детерминированными.

Однако, в природе и в технике гораздо чаще встречаются стохастические системы. В них один, два или более сигналов носят случайный характер. Чаще всего случайными являются возмущающие воздействия, однако шумы случайного характера могут также присутствовать и в сигналах управления. Для стохастического (случайного) сигнала каждая его реализация (при одних и тех же внешних условиях) будет отличаться от предыдущей. Таким образом, нельзя узнать точное значение стохастического сигнала до его реализации.  В детерминированных системах наоборот,  всегда можно предсказать точное значение сигнала при заданных внешних условиях и параметрах системы. Для случайных сигналов x(t) или  x[n]  можно определить только вероятностные характеристики ,  такие как плотность вероятности. Пусть F(y) – интегральная плотность распределения.

F(y)=P{x<y}

где P{x<y} – вероятность того, что x(t) меньше, чем y.

Если для  F(y) существует непрерывная функция w(x) – плотность вероятности,  то верно соотношение:

,

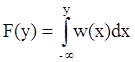где x  - непрерывная случайная величина.

Плотность вероятности называют также дифференциальной плотностью распределения, так как:

Дискретную случайную величину  , которая принимает случайные значения y₁,y₂..y_n… с вероятностью P₁, P₂..P_n… (при условии 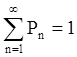) также можно описать через функцию плотности вероятности:

.

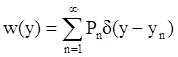Важнейшей характеристикой случайной величины является ее математическое ожидание. Для непрерывной величины она выражается формулой:

,

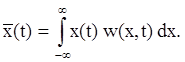для дискретного сигнала:

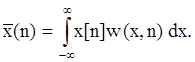
Математическое ожидание среднеквадратичного отклонения от  называется дисперсией:

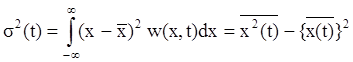
Для решетчатой функции:

Математическое ожидание произведения двух сигналов, один их которых смещен во времени называется взаимной корреляционной функцией.

Для одного сигнала со смещением по времени вводится понятие автокорреляционной функции:

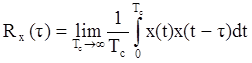
Случайный сигнал считается стационарным, если его автокорреляционная функция не зависит от времени. Стационарные сигналы не затухают и не возрастают неограниченно во времени.