2.Механизмы с постоянной структурой (на примере кулисного механизма).
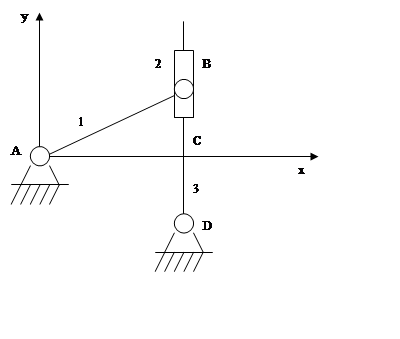
1 – кривошип
2 – камень
3 - кулиса
П = 3 (φz,, y, x), n = 3
p1 = 4 (A, B, C, D)
W = 3n – 2p1 – p2 = 3·3 – 2·4 = 1
или
W = 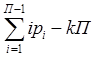 , k = p1 + p2
– n = 4+0-3 = 1
, k = p1 + p2
– n = 4+0-3 = 1
W = 1p1 + 2p2 – 1П = 1·4 + 2·0 – 1·3 = 1,
т.е. подвижность определяется непосредственно по формулам.
3. Механизм переменной структуры.
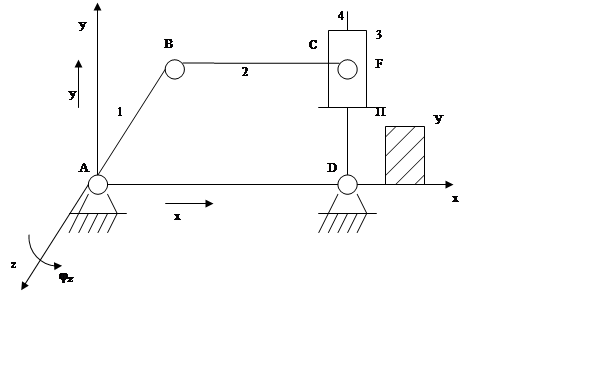
1 – кривошип
2 – шатун
3 – камень
4 – коромысло
О – стойка
У – упор
П - полка
Когда звено 4 не находится на упоре У, камень 3
лежит на полке П ![]() он и звено 4 являются одним
звеном, и механизм является шарнирным четырехзвенником (A, B, C,
D), W = 1.
он и звено 4 являются одним
звеном, и механизм является шарнирным четырехзвенником (A, B, C,
D), W = 1.
Когда звено 4 достигает упора У, оно превращается в стойку, а весь механизм преобразовывается в кривошипно-ползунный (A, B, C, F), W также = 1.
Подвижность простых механизмов с переменной структурой определяется отдельно на каждом этапе их существования по формулам:
(W = 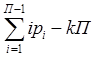 и W
= Пn -
и W
= Пn - 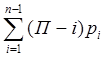 ).
).
4. Механизмы с разомкнутой кинематической цепью.
1, 2, 3, 4 – подвижные звенья,
K, O, L – одноподвижные кинематические цепи
М – трехподвижная кинематическая пара
П = 4 (φx, φy, φz, x)
W = 4n – 3p1 – 2p2 – p3 = 4·4 – 3·3 – 1 = 6
k = p1 + p3 – n = 3 + 1 - 4 = 0,
т.е. в механизме с разомкнутой кинематической цепью
число независимых контуров = 0, и при определении подвижности механизма с
незамкнутыми кинематическими цепями, можно не определить подвижность
пространства, в котором они существуют, так как W = 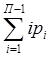
W = 1p1 + 2p2 + 3p3 = 1·3 + 2·0 + 3·1 = 6.
5. Однотипный сложный механизм.
Подвижность сложного механизма определяется подвижностью простых механизмов, входящих в его состав.
Wim = 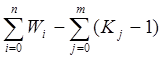 (*),
(*),
где j – индекс общего звена, m – число общих звеньев в сложном механизме, i – индекс простых механизмов, n – число простых механизмов, K – количество присоединенных к одному звену элементарных механизмов.
Если в состав любого сложного механизма входит подвижный механизм, то звено, на котором закреплен этот подвижный механизм, не является присоединенным ( оно звено закрепления), и поэтому оно не учитывается при определении подвижности механизма.
6.Многотипный механизм.
Подвижность сложных многотипных механизмов можно правильно определить только по формуле (*).
7. Комбинированный механизм.
Чтобы определить подвижность комбинированного механизма, необходимо в нем выделить звенья присоединения и закрепления, простые механизмы и механизмы с разомкнутыми кинематическими цепями. Затем определить по формулам
W = Пn - 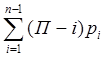 , W
=
, W
= 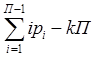 , W =
, W = 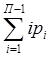
подвижности входящих в его состав простых с разомкнутыми и замкнутыми кинематическими цепями механизмов и значение Кj. И уже потом по (*) найти подвижность комбинированного механизма в целом.
Кинематический анализ машин и механизмов.
Кинематический анализ машин и механизмов заключается в определении координат положений, скоростей и ускорения любых интересующих нас точек механизма.
Кинематический анализ проводится аналитическими и графическими методами.
Аналитические методы имеют высокую точность, позволяют использовать вычислительную технику, но не всегда имеют конечные решения, и чрезвычайно громоздки.
Графические методы просты, наглядны, но имеют малую точность, приемлемая погрешность 5 – 7 %.
Аналоги скоростей и ускорений.
Под аналогом скорости понимают первую производную радиуса вектора (·) по обобщенной координате.
x˙ = ![]() - скорость,
- скорость,
x'φ 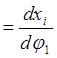 - аналог
скорости
- аналог
скорости
Установим связь между скоростью и ее аналогом. Пусть
i – тая (·) совершает поступательные движения, а
обобщенная координата вращательное, тогда скорость этой точки xi˙ = ![]() домножим
на
домножим
на ![]() .
.
xi = ![]()
![]() = x'φω1
= x'φω1
xi˙ = x'φω1
Аналог ускорения i-той (·) i – го звена называется вторая производная от радиуса вектора по обощенной координате
x''φ
= ![]()
Установим связь между ускорением и его аналогом
x˙˙ = 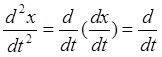 (x'φω1) = ω1
(x'φω1) = ω1 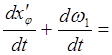 ω1
ω1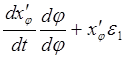 = x''φ
= x''φ![]()
x˙˙= x''φ![]()
Аналитические методы исследования кинематики машин.
В настоящее время существует большое количество методов исследования кинематики машин (Зиновьева, Морошкина, методы аналитической геометрии).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.