Для передачи вращающего движения по заданному закону между валами с параллельными, пересекающимися и перекрещивающимися осями применяются различного вида зубчатые механизмы. При помощи зубчатых колес можно осуществлять передачу движения как между валами с неподвижными осями, так и с перемещающимися в производстве.
Меньшее из двух зацепляющихся зубчатых колес называется шестерней, а большее – зубчатым колесом.
Рейка – частный случай зубчатого колеса, где радиус кривизны равен бесконечности.
К зубчатым механизмам прерывистого движения относятся также механизмы мальтийского креста.
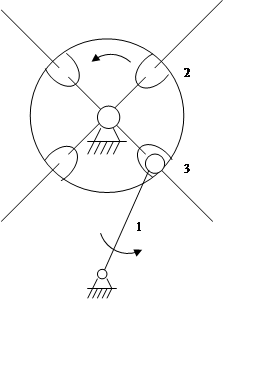
Четырехполостный мальтийский крест:
1 – кривошип;
2 – мальтийский крест;
3 – цевка.
Для осуществления движения только в одном направлении применяют храповые механизмы.
Если необходимо передать на относительно большое расстояние механическую энергию из одной точки производства в другую, то применяют механизм с гибкими звеньями.
Структурный анализ и синтез механизмов.
Структурный анализ занимается тем, что изучает (классифицирует) звенья механизмов, кинематические пары, их соединения между собой, а также определяет подвижность или число степеней свободы механизмов.
Обобщенные координаты механизмов.
Под обобщенными координатами в теоретической механике понимают такие координаты, которые однозначно определяют положение исследуемого объекта в производстве.
В ТММ под обобщенными координатами понимают такие координаты, которые однозначно определяют положение всех звеньев механизма в производстве.
Звенья, которым приписываются обобщенные координаты, называются начальными звеньями.
Число обобщенных координат равно числу степеней свободы механизма или определяет число приводов в двигателях, которые оживляют механизмы.
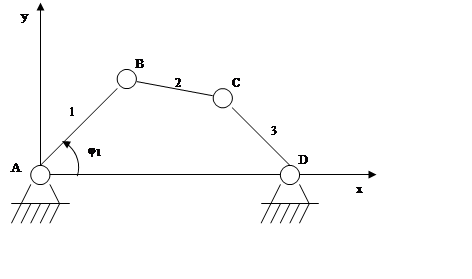
Пусть начальным звеном является звено 1, тогда φ1 – обобщенная координата.
Структурная формула машин и механизмов.
Пусть механизм, имеющий n подвижных звеньев существует в M-мерном и П-подвижном производстве. Найдем W ?
Каждое звено механизма имеет число степеней свободы H = П. При объединении звеньев механизма между собой звенья теряют подвижность или на них накладываются связи.
Wз = Пn (1)
W = Пn-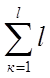 
r (2)
r - сумма
положительных связей.
Представим эту сумму в виде двух сумм:
W = Пn
-
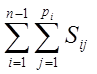(3)
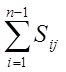- суммируем все связи, которые наклоняют все
одинаковоподвижные кинематические пары.
- суммируем все
связи, которые налагаются разноподвижными кинематическими парами.
Определим число связей, которое налагается одноподвижными парами:
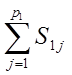= (П – 1)p1,
где p1 – число одноподвижных кинематических пар.
Для двухподвижной пары:
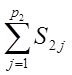= (П – 2)p2
…
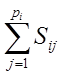= (П – i)pi
(4)
Подставим 4 в 3.
W
= Пn -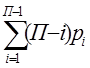 
(5)
П = 5
П = 4
W =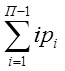 
- kП,
где k – число независимых контуров в структурной схеме механизма (k = p – n, где p – число кинематических пар в механизме).
Под независимым контуром понимают такой контур, в который входит хотя бы одно звено или кинематическая пара, не входящая в другой контур.
W = p1 + 2p2 - 3k.
Примеры определения подвижности механизмов.
Пример 1.
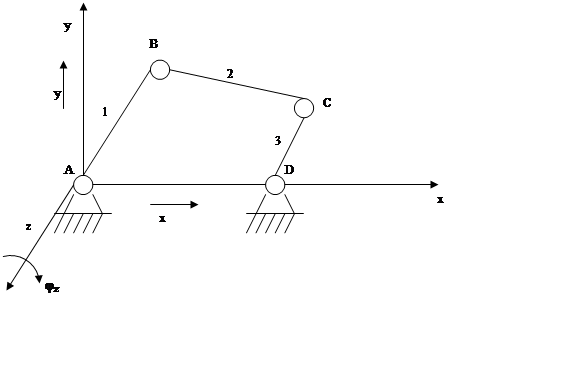φz, x, y
П = 3
n = 3
p1 = 4 (A, B, C, D)
p2 = 0
W = 3·3 – 2·4 = 1
или k = p - n = 4 – 3 = 1
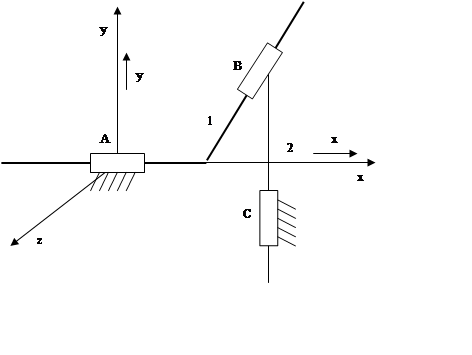
W = 2n – p1
W = 2·2 – 3 =1
K = p – n
W = p1 – k2 = 3 – 2 = 1
Пример 3.
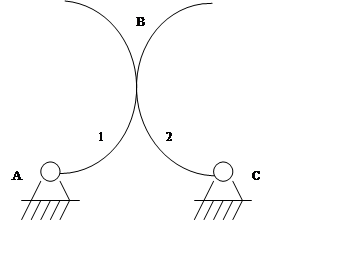
φz, x, y
П = 3
W = 3n – 2p1 – p2
Структурный синтез машин и механизмов.
Под структурным синтезом понимают разработку или создание структурной схемы машины по заданной подвижности.
Структурный синтез ведут с помощью структурных формул, структурных групп или групп Ассура с помощью структурных математических моделей.
Образование механизмов по Ассуру.
В соответствии с Ассуром все механизмы образуются следующим образом: к элементарному механизму (механизму 1-го класса) присоединяются кинематические цепи, обладающие нулевой подвижностью относительно внешних кинематических пар.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.