Алгоритм создания машин и механизмов. Пространство, в котором существуют механизмы. Основные виды механизмов. Аналитические методы исследования кинематики машин, страница 5

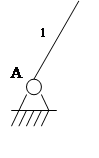
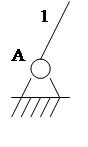
элементарный механизм

(механизм 1-го класса)

+

=

W = 3·2 – 2·3 = 0

W =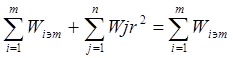

Структурная группа (группа Ассура) – это кинематическая цепь, которая обладает нулевой подвижностью относительно ее внешних кинематических пар и не распадается на более простые цепи, обладающие этими свойствами.

Синтез структурных групп.

1.  Синтез структурных групп ведут по структурным формулам машин и механизмов синтезированием структурных групп машин и механизмов существующих в М = 3 и П = 3 производстве.

p₁ 0

W = 3n – 2p₁ = 0

3n – 2p₁ = 0

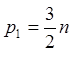
Найдем соотношение между числом кинематических пар и подвижных звеньев.

n	2	4	6	…
p	3	6	9	…

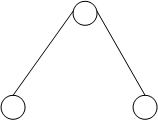
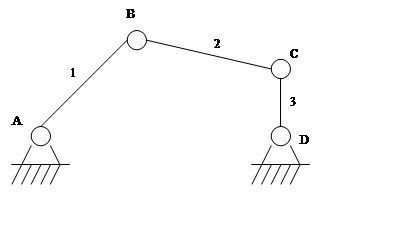
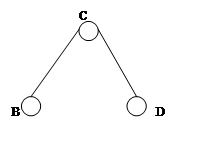
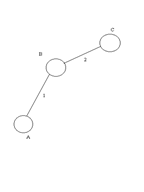
Двухповодковая структурная группа

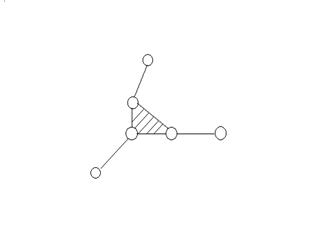
2.  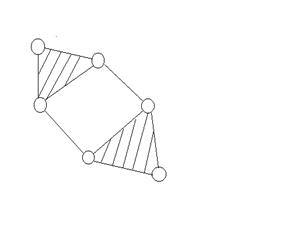Метод развития и перестановки поводка (+ 2 звена и 3 кинематических пары).

3. Метод Добровольского –     «метод  разложения шарнира».

Классификация структурных групп и механизмов.

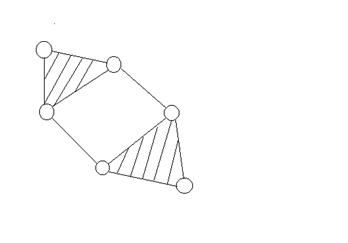
Все структурные графики в соответствии с Ортоболевским Ассуром, разделяют на классы, порядки и вид.

Класс структурной группы определяется числом кинематических пар, образующих замкнутый контур.

Двухповодковая группа отнесена ко II – му классу, а элементарный механизм к механизмам I – го класса.

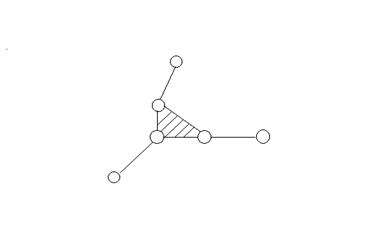
-  III класс, 3 - й порядок.

Порядок группы определяется числом внешних кинематических пар, входящих в группу.

Двухповодковая – 2 – ой порядок.

Двухповодковая группа разделяется на виды в зависимости от расположения вращения и поступления пар.

  

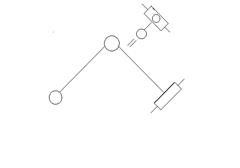
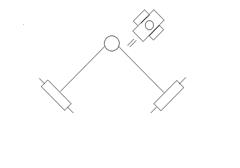
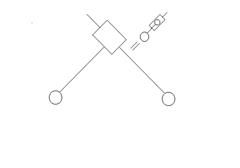
1 вид                            2 вид                                 3 вид                                  4 вид

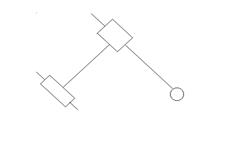
5 вид

6 – го вида не существует, так как это клиновый механизм,       который существует в другом производстве.

Класс механизма определяется наивысшим классом структурной группы, входящей в него.

Примеры структурного анализа.

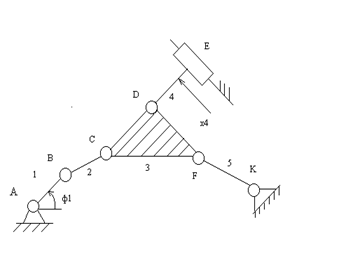            1. Определим подвижность

W  = 3n – 2p₁ – p₂

P₂ = 0

W = 3n – 2p₁ = 3·5 - 2·7 = 1

П = 5

p = p₁ = 7

Выделим элементарный механизм или механизм 1 – го класса.

                 +                                                   

I класс                                                                   структурная группа

                                     III класс,

                                    3 порядок

                                          

                       механизм III – го класса

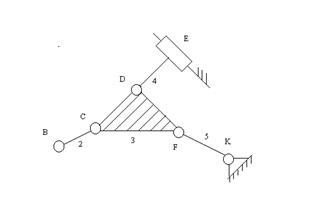
Посмотрим анализ того же механизма, если в качестве начального звена выберем звено 4.

+                                                                          +                                                                                                           

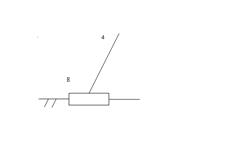
I класс                                    II класс, 2 порядок, 1 вид                 II класс, 2 порядок, 1 вид

Класс механизмов зависит от выбора начального звена.

«Механизмы» с избыточными связями.

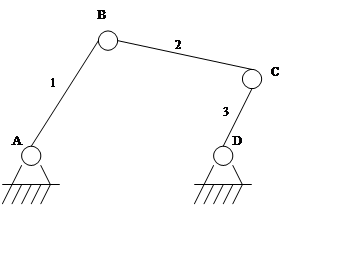
Механизм шарнирного четырехзвенника будет существовать в П=3 пространстве только в том случае, если оси его подвижных пар параллельны. Реальный механизм имеет непараллельные оси и следовательно, он существует в П=6 пространстве.

W = 6n – 5p₁ – 4p₂ – 3p₃ – 2p₄ – p₅

p = p₁ = 4  W = 6·3 – 5·4 = -2

W  0 – ферма статически неопределимая,

W 0  - механизм,

W = 0 – ферма (балка) статически определимая.

Формула показала, что перед нами механизм с избыточными связями.

Для того, чтобы исследуемый шарнирный четырехзвенник превратить в механизм, нужно правильно подобрать кинематические пары.

Сферическая кинематическая пара с пальцем.

W = 6·3 – 5·3 – 4·1  = -1

Сферическая пара.

W = 6·3 – 5·3 – 3·1  = 0

W = 6·3 – 5·2 – 3·2  = 2

….

W = 6·3 – 5·2 – 4·1 - 3·1 = 1

Механизм с избыточными связями является неработоспособным и поэтому избыточные связи в механизмах должны выявляться и устраняться путем правильного подбора кинематических пар.

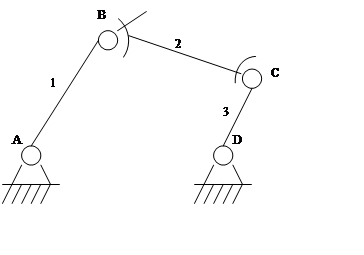
Лишние (или местные) степени подвижности или свободы.

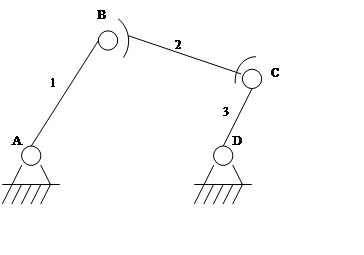
W = 6·3 – 5·2 – 3·2  = 2

Вторая подвижность механизма в данном случае связана с вращением звена 2 вокруг своей оси.