Эта подвижность называется местной, так как она не оказывает никакого влияния на закон движения механизма, а определяет только вращение звена 2.
Местные подвижности обычно полезны для механизмов, их не устраняют, так как они благоприятно действуют на износ в кинематических парах, однако при общем анализе в кинематике местные подвижности не учитывают.
Структурный синтез механизма с помощью математических моделей.
Разработаем структурную математическую модель механизма. Для этого необходимо подсчитать число кинематических пар, которые входят в механизм; определить число подвижных звеньев; найти формулы, определяющие подвижность механизма.
t – вершинное звено.
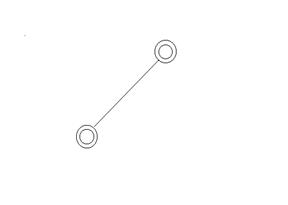
t = 2
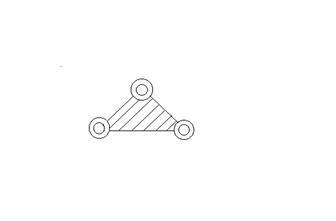
t = 3
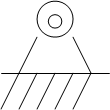
- S - стойка
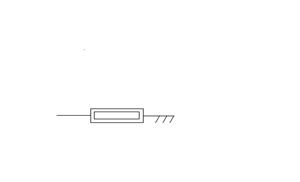
Т – базовое звено
Подсчитаем число кинематических пар, входящих в механизм.
q' = 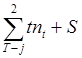 - число элементов
кинематических пар
- число элементов
кинематических пар
j = 0, 1, 2 …
(1)
p = 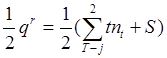 - число кинематических пар
- число кинематических пар
Число подвижных звеньев:
(2)n = ![]()
![]() Сгруппировав 1, 2 и формулы подвижности получим:
Сгруппировав 1, 2 и формулы подвижности получим:
p = 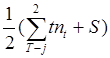
n = ![]() (3)
(3)
W = Пn - 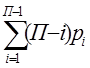
![]() p =
p = 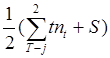
n = ![]()
W = 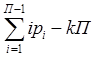 (4)
(4)
k = p – n
p = ![]()
Формулы 3 и 4 полностью адекватны.
Проведем синтез механизмов с помощью структурной математической модели 4.
Пусть необходимо синтезировать механизмы, которые должны существовать в П = 2 производстве, иметь один замкнутый контур (k = 1), содержать в своем составе линейные или двухвершинные звенья (Т = 2) и иметь одну подвижность (W = 1).
Подставим начальные условия синтеза в 4.
![]()
2p = 2n2 + S
n = n2
1 = p1 - 1·2
1 = p-n
p = p1
p = p1 = 3 – число кинематических пар
n = n1 = p – 1 = 2 – число подвижных звеньев
S = 2p – 2n = 2 – число присоединившихся к ст.
Существуют следующие одноподвижные пары.
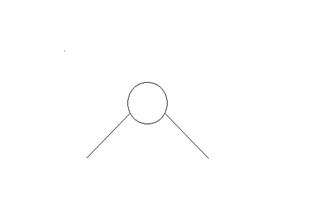
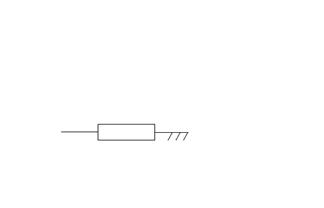
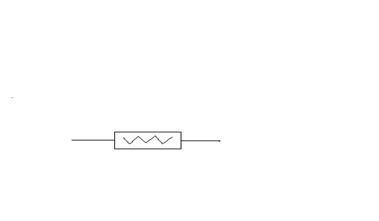
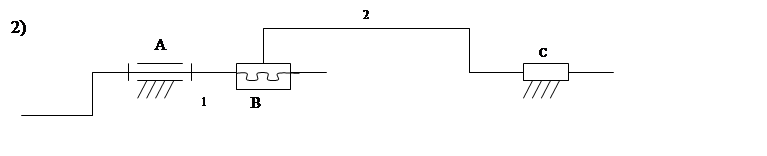
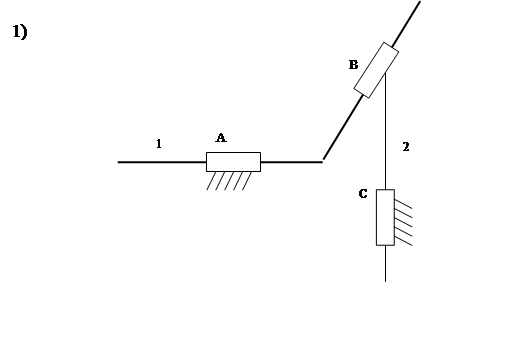 |
и другие…
Структурные математические модели 3 и 4 могут
использоваться для синтеза структурных групп: W = 0
и S![]() S' (число внешних
кинематических пар), n
S' (число внешних
кинематических пар), n![]() n'
(число звеньев, входящих в структурную группу).
n'
(число звеньев, входящих в структурную группу).
Классификация механизмов.
Механизмы подразделяют на: элементарные, простые и сложные; с постоянной структурой и с переменной структурой ; с разомкнутыми кинематическими цепями и с замкнутыми кинематическими цепями (однотипные, многотипные); комбинированные, стационарные, подвижные.
Элементарным называется механизм, который нельзя более расчленить на части, способные самостоятельно преобразовывать движение.
Простой механизм – механизм, состоящий из элементарного механизма + одна структурная группа.
Сложный механизм – механизм, состоящий из элементарного(ых) механизма(ов), к которому(ым) присоединены две или более структурные группы.
Под однотипными сложными механизмами будем понимать механизмы, в состав которых входят только элементарные механизмы и структурные группы, имеющие одинаковые количественные и видовые простейшие перемещения звеньев и элементов кинематических пар.
Под многотипными сложными механизмами будем понимать механизмы, в состав которых входят элементарные механизмы и структурные группы, существующие в различных пространствах.
Механизмами с разомкнутой кинематической цепью называются механизмы, которые имеют в своем составе только разомкнутые кинематические цепи.
Механизмы с постоянной структурой – устройства, кинематическая цепь которых не изменяется в процессе их работы.
Механизмы с переменной структурой – механизмы, кинематическая цепь которых изменяется в процессе их функционирования.
Комбинированные механизмы – механизмы, которые состоят из различных сложных механизмов, как с постоянной, так и с переменной структурой.
Стационарный механизм – простой механизм, если его стойка неподвижна.
Подвижный простой механизм – механизм, если он закреплен на подвижном звене другого механизма.
Рассмотрим примеры определения подвижности различных механизмов.
1. Элементарные механизмы.
Элементарные механизмы представляют собой простейшие механизмы с независимой кинематической цепью. Подвижность элементарных механизмов определяется подвижностью, входящей в них кинематической парой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.