Теплоемкость металлов. Теория теплоемкости кристаллической структуры. Теплоемкость электронного газа. Электронная теплопроводность металлов, страница 6

Тепловая энергия передается решеткой путем тепловых колебаний атомов, в результате чего в теле по всем направлениям распространяются упругие волны, которые отличаются не только направлением, но и длиной волны. Наиболее длинные волны имеют скорость распространения, равную скорости звука, величина которой может быть рассчитана по формуле

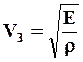                                                                                   (3.5)

где Е – модуль сжатия; ρ – плотность материала.

Наиболее короткие волны, на долю которых приходится основной объем тепловой энергии, имеют скорость порядка 60% от скорости звука, а ее длина примерно равна удвоенному расстоянию между соседними атомами. Длина коротких волн примерно равна удвоенной величине межатомного расстояния.

Скорость распространения волн связана с их длиной и частотой колебания соотношением

                                                                                    (3.6) 

где  λ_В –длина волны; ν – частота колебания.

Если исходить из этих скоростей распространения тепловых  волн, то теплопроводность твердых тел должна быть очень велика, а время установления теплового равновесия мало, что не согласуется с обширным экспериментальным материалом.  Причину этого несоответствия раскрывает теория П. Дебая, согласно которой скорость распространения тепловых волн замедляется из-за тепловых флуктуаций, связанных с ангармоничностью колебаний атомов в решетке и несовершенств кристаллического строения.  Особенно сильное рассеивание испытывают короткие волны, для которых реальные металлы не являются «прозрачной» средой. Интенсивность волн при прохождении пути длиной Х  падает по экспоненциальному закону (закон Бугера)

                                                                        (3.7)

где μ – коэффициент рассеивания фоновой волны, который зависит от длины волны и «прозрачности» среды.

Теоретически решеточная теплопроводность определяется выражением

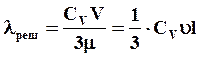                                                                (3.8)

где С_V – теплоемкость решетки; υ – скорость звука;  l - средняя длина свободного пробега фонона между двумя актами переброса.

В процессе теплового переброса участвуют не все фононы, а только те, средняя энергия которых не менее

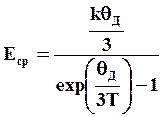                                                                                                    (3.9)

где  θ_Д – характеристическая температура Дебая.

Из (3.8) и (3.9) следует, что при высоких температурах (выше характеристической), когда теплоемкость С_V  постоянна, длина свободного пробега фонона зависит от избытка его энергии и количества фононов, которое при высокой температуре пропорционально Т. Поэтому длина пробега и решеточная теплопроводность будут обратно пропорциональны температуре. При низких температурах    энергия фонона пропорциональна  exp[-θ_Д/(3T)], соответственно этому теплопроводность  будет обратно пропорциональна выражению

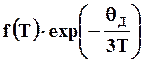
где f(T) – функция, учитывающая температурную зависимость теплопроводности.

При достаточно низких температурах плотность фононного газа убывает, поэтому все большее значение начинают играть столкновения фононов с границами зерен кристалла. Когда эти столкновения становятся преобладающими, коэффициент теплопроводности начинает зависеть от формы образца, что соответствует переходу от плотного фононного газа к заряженному и к состоянию вакуума. В этом случае длина свободного пробега фонона становится сравнимой с размером образца, и теплопроводность теряет смысл как теплофизическое свойство материала. Так как при низких температурах теплоемкость пропорциональна Т³, то и теплопроводность решетки будет связана с температурой такой же кубической зависимостью.

3.3.  Электронная теплопроводность металлов