Теплоемкость металлов. Теория теплоемкости кристаллической структуры. Теплоемкость электронного газа. Электронная теплопроводность металлов, страница 3

В теории Дебая общая тепловая энергия кристалла представляется как сумма энергий всех различных типов гармонических колебаний, каждый из которых имеет свою частоту. Напомним, что в теории Эйнштейна общая тепловая энергия определялась как сумма энергий всех атомов кристалла. Частоты не могут принимать любые значения – они квантованы,  следовательно, квантуется и энергия колебаний. Тогда полная энергия вычисляется как

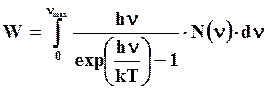                                                           (2.17)

где N(ν) – плотность колебательных (частот) состояний, а N(ν)^.dν – число колебаний с частотой от ν до ν +dν.

Согласно допущению Дебая

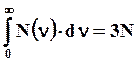
Опуская дальнейшие выкладки, приведем конечное выражение для теплоемкости

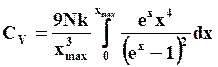                                                                   (2.18)

где 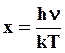 ;  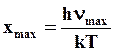; ν_max – верхний максимальный предел собственных частот колебаний отдельный атомов кристалла.

Введем величину

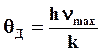
имеющую размерность температуры и называемую характеристической температурой Дебая. При высоких температурах, когда T >> θ_Д, а x_max << 1 теплоемкость будет равна 3R, т.е. совпадать с теплоемкостью, выраженной законом Дюлонга-Пти. В области низких температур, когда T << θ_Д или x_max >>1 теплоемкость будет определяться выражением

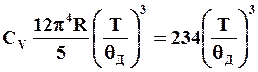                                                           (2.19)

которая с достаточной точностью описывает теплоемкость твердого тела при низких температурах.

Значения характеристической температуры Дебая для некоторых химических элементов представлены в таблице 2.1.

Таблица 2.1

Температура Дебая(град.К)  для некоторых химических элементов

2.3.  Теплоемкость электронного газа

Согласно статистике Ферми-Дирака, важнейшим свойством электронного газа по сравнению с классическим  является его малая чувствительность к нагреву. При повышении температуры металла тепловому возбуждению подвергаются не все электроны, составляющие электронный газ, а только те, энергия которых близка к энергии Ферми. Эта предельная энергия при температуре абсолютного нуля оказывается равной

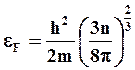                                                                                (2.20)

где m – масса электрона; n – число электронов в единице объема.

В статистике Ферми-Дирака твердое тело рассматривается как некоторая квантовая система, в которой частицы размещаются по различным энергетическим состояниям, а функция их распределения отвечает равновесному (наивероятнейшему) состоянию системы. Таким образом, функция распределения характеризует степень вероятности заполнения электронами конкретного квантового состояния внутри сферы Ферми. Энергетически полностью заполненному уровню соответствует функция распределения f = 1,  полностью пустому f = 0, а промежуточное значение f – состоянию заполненному частично. Функция распределения электронов по энергиям имеет вид

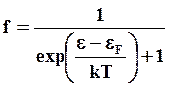                                                                     (2.21)

а ее графический вид представлен на рис. 2.3.

По мере возрастания температуры кривая f(ε) становится более пологой, состояния с энергией порядка kT, меньшей ε_F, начинают освобождаться, а состояния с энергией порядка kT, большей ε_F, начинают заполняться электронами.

Качественно теплоемкость электронов может быть найдена из следующих рассуждений. Из  рис. 2.3.б следует, что при увеличении температуры от 0 до Т энергия одного электрона возрастает на величину порядка kT (kT/ε_F), где отношение  kT/ε_F  определяет долю электронов, испытывающих тепловое возбуждение. Увеличение энергии грамм-атома металла благодаря вкладу электронов составит RT (kT/ε_F). Тогда вклад электронов в теплоемкость окажется равным