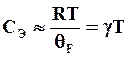Теплоемкость металлов. Теория теплоемкости кристаллической структуры. Теплоемкость электронного газа. Электронная теплопроводность металлов, страница 4

                                                                                (2.22)

где 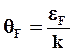 - температура Ферми; γ – коэффициент электронной теплоемкости.

Рис. 2.3. Функция распределения электронов по энергиям

Физическая теория дает следующее выражение для расчета коэффициента электронной теплоемкости

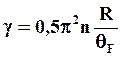                                                                                     (2.23)

где n – число коллективизированных электронов, приходящихся на один атом.

У металлов θ_F = (10⁴…10⁵)^оК, поэтому при комнатных температурах вклад электронов в  молекулярную теплоемкость незначителен порядка 10^-2R.

2.4. Теплоемкость реальных металлов

Теплоемкость реальных металлов отличается от теоретической в результате следующих факторов: наличия ангармонических колебаний, дефектов кристаллического и различного рода разупорядоченностей.

В реальных металлах атомы совершают не гармонические (ангармонические) колебания в силу целого ряда причин. Ангармонизм колебаний увеличивает теплосодержание материала, при этом дополнительный вклад в удельную теплоемкость по сравнению с теоретической можно определить по формуле

где g ≈ (3…8)^.10^-4  Дж/(моль^.К⁴) – коэффициент ангармонических колебаний.

Влияние  ангармонических колебаний наиболее ощутимо при высоких температурах. В общем случае повышение теплоемкости за счет ангармонических колебаний не превышает 10%.

Вакансии всегда присутствуют в кристаллической решетке реального металла, при этом существует так называемая равновесная концентрация вакансий, при которой свободная энергия структуры достигает минимального значения. Равновесная концентрация вакансий связана с температурой следующей зависимостью

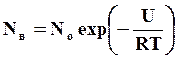
где 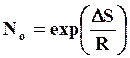 - энтропийный множитель; ΔS – энтропия образования вакансии; U – энергия образования кавансии.

Дополнительная энтальпия при образовании вакансий определится как

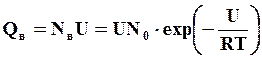
тогда дополнительная теплоемкость за счет вакансий определится

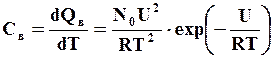
В общем случае с повышением температуры вакансионная теплоемкость возрастает и принимает ощутимые значения вблизи температуры плавления металла. Можно выделить группу металлов, у которых вакансионная теплоемкость принимает наибольший прирост с повышением температуры. К ним можно отнести Mo, W, Ta, Nb и другие.

В реальных металлах всегда присутствуют дислокации, наличие которых повышает энтальпию материала за счет упругой энергии, концентрируемой вокруг линейного дефекта кристаллического строения. Повышение энтальпии за счет увеличения плотности дислокаций можно оценить по формуле

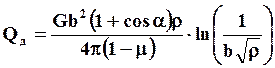
где  G – модуль сдвига;  b – вектор Бюргерса; α – угол между вектором Бюргерса и осью дислокации;  ρ – плотность дислокаций.

С повышением температуры дополнительная теплоемкость за счет дислокаций снижается в связи с уменьшением плотности дислокаций. Учитывая, что плотность дислокаций повышается при пластической деформации и закале, теплоемкость наклепанной и закаленной структуры  выше по сравнению с отожженной.

2.5. Электронная теплоемкость реальных металлов

Электронная теплоемкость определяется выражением

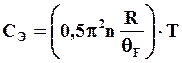
где n – число коллективизированных электронов, приходящихся на один атом; 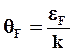 - температура Ферми (ε_F – энергия Ферми; k – постоянная Больцмана).

 Число коллективизированных электронов и энергия Ферми зависят от типа химического элемента. Электронная теплоемкость является индивидуальной характеристикой химического элемента. Химические элементы одной группы таблицы Менделеева имеют близкие значения электронной теплоемкости. Чем ниже валентность металла, тем меньше электронная теплоемкость. Переходные металлы обладают более высокой теплоемкостью по сравнению с простыми (щелочными и щелочноземельными) металлами.

2.6.  Сводные результаты