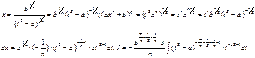 (1)Функция
F(x) называется первообразной для функции f(x) на
интервале (a,b), если в любой точке х интервал (a,b)
функция F(x) дифференцируема и имеет производную F’(x),
равную f(x).
(1)Функция
F(x) называется первообразной для функции f(x) на
интервале (a,b), если в любой точке х интервал (a,b)
функция F(x) дифференцируема и имеет производную F’(x),
равную f(x).
Совокупность всех первообразных функций для данной функции f(x) на интервале (a,b) называется неопределённым интегралом от функции f(x) и обозначается символом ∫f(x)dx.
Свойства неопределённого интеграла:
1)(∫f(x)dx)’=f(x)
Док-во: (∫f(x)dx)’=(F(x)+c)’=f(x)
2)Знак дифференциала перед знаком интеграла уничтожает последний: d∫f(x)dx=f(x)dx
Док-во: d∫f(x)dx=(∫f(x)dx)’dx=f(x)dx
3)Знак интеграла перед знаком дифференциала уничтожает последний, но при этом вводится произвольное постоянное слагаемое: ∫dF(x)=F(x)+C
Док-во: ∫dF(x)=∫f(x)=F(x)+C
4)Постоянный множитель можно выносить за знак интеграла: ∫аf(x)dx=a∫f(x)dx
Док-во: (∫af(x)dx)’=af(x); (a∫f(x)dx)’=a(∫f(x)dx)’=af(x)
5)Неопределённый интеграл алгебраической суммы равен сумме интегралов от каждого слагаемого в отдельности: (∫(f(x)±φ(x))dx)’ = f(x)±φ(x); (∫f(x)dx±∫φ(x)dx)’=f(x)±φ(x)
Теорема: Если f(x) – функция непрерывная, то неопределенный интеграл существует.
Неберущиеся
интегралы: ![]()
(2) 1)∫UdV=UV-∫VdU
Док-во: d(UV)=UdV+VdU; UV=∫UdV+∫VdU; ∫UdV=UV-∫VdU
![]() 2)
2)
![]()
Док-во: d(UV)=UdV+VdU;
![]() Основные рекомендации:
Основные рекомендации:
(3) 1)Теорема: Пусть функция t=φ(x) будет определена и имеет непрерывную производную φ’(x) на некотором множестве Х. Т-множество значений функции. Тогда, если для функции g(t), первообразная будет G(t), то для функции g(φ(x))φ’(x), первообразная будет G(φ(x)).
![]() Док-во: Для док-ва этого утверждения достаточно
воспользоваться правилом дифференцирования сложной функции:
Док-во: Для док-ва этого утверждения достаточно
воспользоваться правилом дифференцирования сложной функции:
и учесть, что по определению первообразной G’(t)=g(t).
![]() 2)Терема: Если функция f(x)
непрерывна на [a,b], а функции φ(t), φ’(t) непрерывны
на [α,β], причём a=φ(α), b=φ(β), тогда
2)Терема: Если функция f(x)
непрерывна на [a,b], а функции φ(t), φ’(t) непрерывны
на [α,β], причём a=φ(α), b=φ(β), тогда
![]() Док-во: F(x) – первообразная для f(x),
тогда F(φ(t)) будет первообразной для f(φ(t))∙φ’(t).
Док-во: F(x) – первообразная для f(x),
тогда F(φ(t)) будет первообразной для f(φ(t))∙φ’(t).
(F(φ(t)))t’=F’(φ(t))∙φ’(t)=f(φ(t))∙φ’(t);
![]()
![]()
![]() (4) 1)Рациональным корнем R(x) или
дробно-рациональной функцией называется функция R(x) = Pn(x) / Qm(x). Если n≥m, то дробь неправильная. 2)Всякую правильную
рациональную дробь R(x)=P(x)/Q(x) можно представить в виде суммы простейших дробей
четырёх типов:
(4) 1)Рациональным корнем R(x) или
дробно-рациональной функцией называется функция R(x) = Pn(x) / Qm(x). Если n≥m, то дробь неправильная. 2)Всякую правильную
рациональную дробь R(x)=P(x)/Q(x) можно представить в виде суммы простейших дробей
четырёх типов:
Это разложение зависит от разложения знаменателя на множители:
Q(x)=(x-a)k…(x-b)l(x2+px+q)m…(x2+rx+s)n;
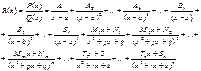
Если R(x) – неправильная дробь, то нужно разделив числитель на знаменатель, представить дробь как сумму многочлена (целая часть) и правильной дроби.
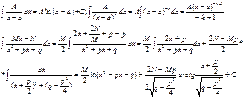 3)
3)
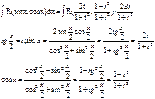 (5)I.
(5)I.
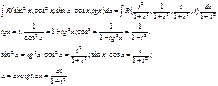 II.
II.
(6)1)I. ∫R(x,xr1/s1,xr2s2,…,xrn/sn)dx=∫R(tN,tr1∙a1,…,trn∙an)NtN-1
Обозначим наименьший общий знаменатель r1/s1,r2/s2,…rn/sn через N:
N(ri/si)=ri∙ai; xri / si = (tN)ri / si = tri∙a
Теперь каждая дробная степень t выражается через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию от t.
![]() II.
II.
- интеграл сводится к
линейному от рациональной функции.
![]() 2)∫xm(axn+b)pdx. Можно
доказать, что интеграл берётся только в следующих 3 случаях: I)p-целое.
В этом случае интеграл сводится к первому случаю; II)(m+1)/n – целое, p=r/s; axn+b=tS; (axn+b)p=tSr/S=tr;
2)∫xm(axn+b)pdx. Можно
доказать, что интеграл берётся только в следующих 3 случаях: I)p-целое.
В этом случае интеграл сводится к первому случаю; II)(m+1)/n – целое, p=r/s; axn+b=tS; (axn+b)p=tSr/S=tr;
III)((m+1)/n) + p – целое; axn+b=tSxn;
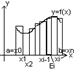
 (7)Криволинейной трапецией называется фигура, которая
снизу ограничена осью Ox, сверху графиком функции y=f(x), а
слева и справа прямыми x=a, x=b
(7)Криволинейной трапецией называется фигура, которая
снизу ограничена осью Ox, сверху графиком функции y=f(x), а
слева и справа прямыми x=a, x=b
![]()
ΔSi=f(Ei)∙(xi-xi-1);
Найти площадь криволинейной трапеции.
Дано: 1)x€[a,b]; 2)f(x)-ограниченная
Решение: 1)Разобьём отрезок [a,b] на n-частей; a=x0<x1<…<xn=bj;
xi-xi-1=Δxi 2)Ei €[xi-1,xi],i=от1,до n; 3)f(Ei),i=от1, до n;
4)f(Ei)Δxi,i=от1,до n;
![]()
![]()
Криволинейным сектором называется плоская фигура, ограниченная кривой L и двумя лучами, составляющими с полярной осью углы α и β.(!)
 (8)
(8)
![]()
Если этот предел существует и не зависит от способа разбиения [a,b] на части и выбора точки Ei, то он называется определённым интегралом от функции f(x) на [a,b]. Обозначение: ∫baf(x)dx, x – переменная интегрирования, f(x) – подынтегральная функция, a и b – пределы интегрирования. С точки зрения геометрии, определённый интеграл ∫baf(x)dx – это площадь криволинейной трапеции. Функция f(x) называется интегрируемой на [a,b], если существует определённый интеграл.
![]()
(*)
Если для функции f(x) предел (*) существует, то функцию называют интегрируемой на отрезке [a,b].
Классы интегрируемых функций:
1)функция, непрерывная на [a,b], интегрирована на этом отрезке.
2)функция, кусочно-интегрированная на [a,b] (имеющие конечное число точек разрыва I рода), интегрируемы на [a,b].
3)функции, кусочно-монотонные и ограниченные на [a,b] также интегрированы на [a,b].
(9)Свойства определённого интеграла:
1)Если функции f(x) и g(x) интегрируем на сегменте [a,b], то функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.