(20)A(x-x0)+B(y-y0)+C(z-z0)=0
Уравнение плоскости, проходящей через точку М0(x0,y0,z0) можно записать как z-z0=A(x-x0)+B(y-y0).
Касательной плоскостью к поверхности z=z(x,y) в точке М0 называется плоскость, в которой лежат все касательные, проведенные к любой кривой в точке М0, лежащей на этой поверхности.
(21)Понятие экстремума ф. двух переменных:
Функция z=f(x,y) имеет максимум(минимум) в точке М0(x0,y0), если f(x0,y0)>f(x,y) (f(x0,y0)<f(x,y)) для всех точек (x,y) в окрестности этой точки.
Необходимое условие существования экстремума:
Если z=z(x,y) имеет в точке M0(x0,y0) экстремум, то обе частные производные в этой точке либо равны 0, либо не существуют.
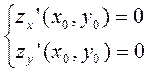 Док-во:
Док-во:
Рассмотрим функцию z=z(x,y)
z=z(x,y0)
Мы получили функцию одной переменной х, которая при х=х0 имеет экстремум, тогда
![]()
![]() Аналогично можно доказать, что
Аналогично можно доказать, что
Достаточное условие существования экстремума:
Если функция z=z(x,y) удовлетворяет следующим условиям:
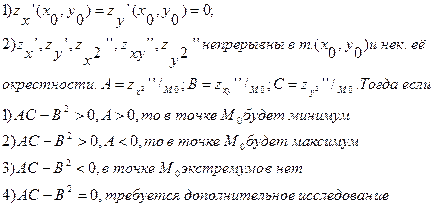
(25)вычисление ∫∫∫ в декартовых координатах
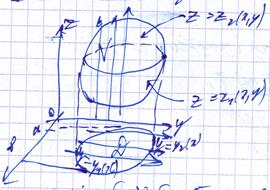
Пусть область V будет правильной в направлении оси Oz.
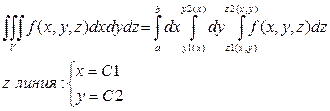
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.