Движение жидкости в напорном трубопроводе, страница 2

а - центробежный насос; b - всасывающий трубопровод;

с - клапан с решеткой;  - расстояние от уровня воды в водоеме до оси насоса

При заданном расходе Q среднюю скорость потока в трубе V обычно принимают в пределах  м/с. Задавшись скоростью, можно определить площадь сечения всасывающей трубы:

                                                                         

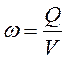
При известном расходе Q во всасывающем трубопроводе диаметр этого трубопровода будет

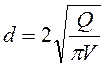.                                                           (5.4)

Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с уровнем воды в водоеме и сечением 1-1, где давление  равно атмосферному , а скорость . Сечение 2-2 принимаем на всасывающем трубопроводе на входе в насос:

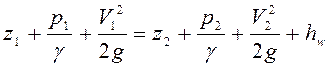,                     (5.5)

где ;  - высота всасывания, т.е. расстояние по вертикали от плоскости 1-1 до оси насоса;  - скорость на входе в насос и в самой всасывающей трубе;  - суммарные потери напора в трубе.

Давление в сечении 2-2 принимаем равным абсолютному, т.е. .

Суммарные гидравлические потери в трубопроводе

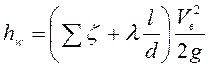,                                         (5.6)

где  - средняя скорость потока трубе, ;  - коэффициент гидравлического трения; , d - длина и диаметр трубопровода соответственно;  - сумма коэффициентов местных сопротивлений трубопровода.

Абсолютное давление на входе в насос  ( - вакуумметрическое давление на входе в насос). Уравнение Бернулли можно записать как

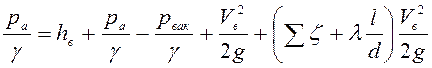             (5.7)

или

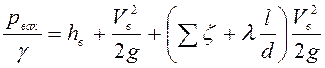.                                        (5.8)

Обозначим 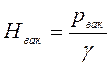,  - вакуумметрический напор.

 применительно к лопастному насосу называется вакуумметрической высотой всасывания.  зависит от конструктивных особенностей насоса и расхода, .

Из уравнения (5.8) можно определить высоту всасывания насоса:

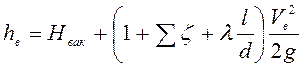.                         (5.9)

Таким образом, высота всасывания  насоса зависит от вакуумметрической высоты всасывания насоса и гидравлических потерь во всасывающем трубопроводе.

Вакуумметрическая высота всасывания  определяется по кавитационной характеристике насоса.

♦ Пример 5.1

Вода ( °С) из водонапорной башни подается в приемный резервуар по новому трубопроводу из сварных стальных труб диаметром d длиной  м. На трубопроводе имеется задвижка, обратный клапан.

Определить диаметр трубопровода при условии открытия задвижки на 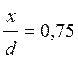 и обеспечении расхода  л/с. Разность уровней воды в башне и резервуаре считать постоянной и равной  м (рис. 5.2).

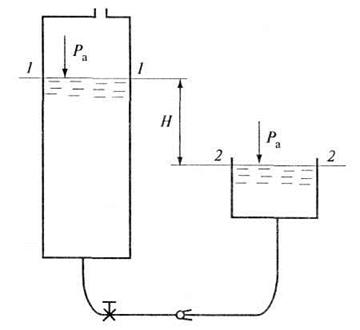
Рис. 5.2. К примеру 5.1

Составив уравнение Бернулли для сечений 1-1 и 2-2, проведя плоскость сравнения по сечению 2-2, получим , где  - гидравлические потери в трубопроводе:

.

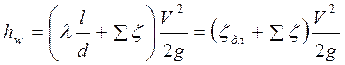Средняя скорость в трубопроводе

.

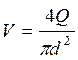Коэффициент гидравлического трения находим по формуле 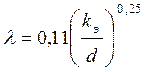 для квадратичной области сопротивления.

Шероховатость сварных стальных труб  мм (см. табл. 3.1).

Сумма коэффициентов местных сопротивлений

,

где  - коэффициент сопротивлений на входе в трубу из резервуара;  - сопротивление обратного клапана;  - сопротивление задвижки;  - сопротивление колена;  - сопротивление на выходе из трубы в резервуар.

По табл. П1.4 приложения находим значения :

; ; ; .

В табл. 4.2 находим  при открытии на 0,75: .

.

Коэффициент сопротивления системы

.

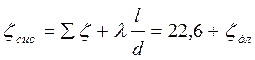Задаемся разными диаметрами d, определим , среднюю скорость,  и потери напора .

Вычисления сводим в табл. 5.1.

Таблица 5.1

№ п/п	d, м				V, м/с
1	0,2	0,0145	8,7	31,3	2,55	11,37
2	0,225	0,0141	7,52	30,12	2,01	6,82
3	0,25	0,0137	6,57	29,17	1,63	4,43
4	0,275	0,0134	5,83	28,43	1,35	2,64

Строим график  (рис. 5.3). На графике по вертикальной оси откладываем  м, проводим горизонтальную линию до пересечения с кривой .

Сносим полученную в результате пересечения точку на горизонтальную ось d, получаем  м. Согласно ГОСТ на стальные трубы ближайший внутренний диаметр (условный проход)  мм. Принимаем мм.