Движение жидкости в напорном трубопроводе, страница 11

Путем регулирования задвижки можно получить как максимальное, так и минимальное водопотребление в точке 3.

♦ Пример 5.7

Определить диаметры отдельных участков разветвленной водопроводной сети (рис. 5.14) и напор в начальной точке 1 сети так, чтобы напоры в конечных узловых точках 5, 6, 7 и 4 были бы не меньше свободного напора  м. На рисунке представлены расходы Q (л/с) и длины  (м).

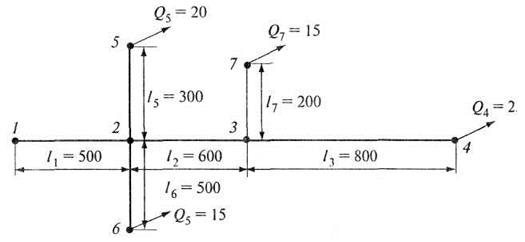
Рис. 5.14. К примеру 5.7

В данной задаче заданы лишь две величины (расходы и длины участков), поэтому необходимо задаться третей величиной, т.е. диаметрами участков. Удобнее задать диаметры участков исходя из предельно допустимых расходов в водопроводных трубах (см. табл. 5.3).

Главная магистраль водопроводной сети 1-2-3-4.

Расход в начальной точке 1  л/с.

Транзитные расходы отдельных участков сети, л/с:

; .

Таблица 5.5 - Результаты расчета

Q, л/с	d, м	А, с2/л6
75	0,25
40	0,2
25	0,175

По значению путевых расходов выбираем диаметры участков главной магистрали и соответствующие им удельные сопротивления. Результаты сводим в табл. 5.5.

Далее определяем потери напора на отдельных участках магистрали:

 м;

 м;

 м.

По условию задачи в узловых точках свободный напор  м.

Напоры в точках главной магистрали:

 м;

 м;

 м.

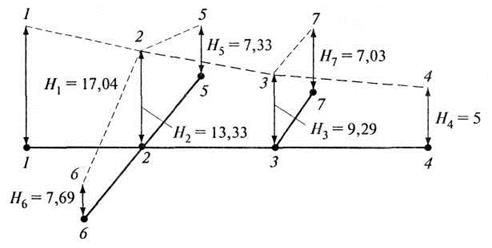
Рис. 5.15. Пьезометрические линии сети

На рис. 5.15 показана пьезометрическая линия главной магистрали 1-2-3-4 и отводов магистрали 2-5, 2-6 и 3-7.

Расчет отводов 2-5, 2-6 и 3-7.

Для того чтобы в узле 5 иметь напор , на участке 2-5 гидравлические потери напора должны равняться :

 м.

Зная потери, определяем удельное сопротивление участка 2-5:

c²/л⁶.

По табл. 5.3 принимаем ближайший по значению диаметр  м, для этого диаметра  с²/л². Тогда действительные по значению потери напора вдоль этого участка будут равны

 м,

а напор в узле 5

 м.

Подобным образом рассчитываются ответвления 2-6 и 3-7. Результаты вычислений сведены в табл. 5.6.

Таблица 5.6 - Результаты расчета

Участок	, м	, л/с	А, с2/л6	, м	d, м	, м
2-5	300	20		6,0	125	7,33
2-6	500	15		5,64	125	7,69
3-7	200	15		2,26	125	7,03

В узлах 5, 6, 7 полученные напоры Н больше свободного напоpa м.

5.7. НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ В ТРУБАХ

Неустановившееся движение - движение, когда скорость и давление в отдельных точках потока жидкости изменяются по времени. В этом случае скорость и давление являются функцией не только положения ее отдельной точки относительно выбранных координат, но и времени. Следовательно, средняя скорость в живом сечении потока и расход его изменяются по времени.

В практике эксплуатации систем водоснабжения и водоотведения достаточно часто встречаются случаи неустановившегося движения потоков. Неустановившееся движение наблюдается как в напорных трубах, так и в открытых руслах.

В напорных трубах поток жидкости ограничен жесткими стенками. Площадь живого сечения потока не зависит от времени и может являться функцией расстояния вдоль трубы, т.е. . На расход Q расстояние  не влияет. Расход жидкости зависит от времени, т.е. . Однако скорость связана с площадью сечения, следовательно, .

Средняя скорость потока для данного момента времени

.

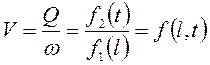Для получения уравнения, описывающего изменения гидродинамических характеристик потоков при неустановившемся движении, используется уравнение неустановившегося движения для элементарной струйки несжимаемой жидкости.

Уравнение неустановившегося движения для элементарной струйки вязкой несжимаемой жидкости записывается в виде уравнения Бернулли для двух живых сечений 1-1 и 2-2:

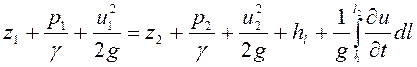,     (5.45)

где  - потери напора по длине струйки между сечениями.

Интеграл 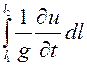 по аналогии с другими слагаемыми уравнения Бернулли называют инерционным напором .