






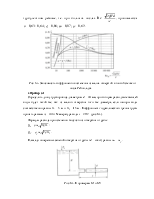

























Глава 6. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
6.1. ОБЩИЕ СВЕДЕНИЯ И ОСНОВНЫЕ
ХАРАКТЕРИСТИКИ ИСТЕЧЕНИЯ
Истечение жидкости из какого-либо резервуара может происходить через отверстия различных размеров и форм, насадки и короткие трубы в различных условиях.
На рис.
6.1 изображен резервуар, в вертикальной боковой стенке его имеется малое
отверстие. Истечение из отверстия может быть при постоянном напоре Н и
давлении ![]() на поверхности жидкости в резервуаре.
на поверхности жидкости в резервуаре.
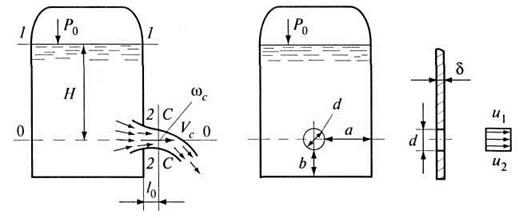
Рис. 6.1. Истечение жидкости из малого отверстия
Н - заглубление центра отверстия диаметром d под уровень свободной поверхности.
Если Н и ![]() являются переменными во времени,
истечение будет переменным, а движение жидкости станет неустановившимся.
являются переменными во времени,
истечение будет переменным, а движение жидкости станет неустановившимся.
Струя из отверстия может истекать в атмосферу или под уровень жидкости, когда вытекающая струя будет распространяться в каком-то другом резервуаре или сосуде, в котором находится жидкость.
При истечении в атмосферу отверстие будет незатопленным, так же как и струя, вытекающая из него. Когда истечение происходит под уровень жидкости, отверстие является затопленным.
Отверстие в резервуаре называется малым, если во всех точках отверстия давление можно считать практически постоянным. Поэтому скорости в разных точках живого сечения струи будут одинаковыми.
Обычно к
малым отверстиям относятся такие, если диаметр 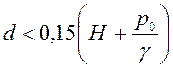 или
гидравлический диаметр
или
гидравлический диаметр ![]() для других форм отверстий.
для других форм отверстий.
Отверстием
в тонкой стенке называется отверстие, когда толщина стенки резервуара ![]() не влияет на условия истечения струи. При
истечении жидкости потери напора в этом случае практически аналогичны местным
потерям в результате внезапного сужения потока. Обычно к отверстиям в тонкой
стенке относят случаи, когда
не влияет на условия истечения струи. При
истечении жидкости потери напора в этом случае практически аналогичны местным
потерям в результате внезапного сужения потока. Обычно к отверстиям в тонкой
стенке относят случаи, когда ![]() .
.
Струя
жидкости при истечении из отверстия на расстоянии ![]() от
входа резко сжимается. На этом расстоянии возникает сжатое сечение С-С (см.
рис. 6.1), площадь живого сечения
от
входа резко сжимается. На этом расстоянии возникает сжатое сечение С-С (см.
рис. 6.1), площадь живого сечения ![]() . Как показали опыты,
расстояние до сжатого сечения составляет
. Как показали опыты,
расстояние до сжатого сечения составляет ![]() . Сжатие
струи происходит в результате сил инерции, действующих на частицы жидкости,
движущиеся по разным траекториям к самому отверстию. Частицы жидкости, обтекая
кромки отверстия, имеют плавную траекторию движения и образуют поверхность
струи на участке длиной
. Сжатие
струи происходит в результате сил инерции, действующих на частицы жидкости,
движущиеся по разным траекториям к самому отверстию. Частицы жидкости, обтекая
кромки отверстия, имеют плавную траекторию движения и образуют поверхность
струи на участке длиной ![]() , на котором имеет место
резкое изменение течения. В сечении С-С происходит практически
параллельноструйчатое течение, т.е. движение, когда линии тока жидкости
параллельны друг другу. Эпюра скоростей в этом сечении весьма близка к
прямоугольной форме. За сжатым сечением струя попадает под действие силы
тяжести.
, на котором имеет место
резкое изменение течения. В сечении С-С происходит практически
параллельноструйчатое течение, т.е. движение, когда линии тока жидкости
параллельны друг другу. Эпюра скоростей в этом сечении весьма близка к
прямоугольной форме. За сжатым сечением струя попадает под действие силы
тяжести.
Коэффициент
сжатия струи ![]()
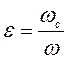 . (6.1)
. (6.1)
На сжатие
струи влияют границы стенок, которые могут находиться достаточно близко к
отверстию. Опытами установлено, что если расстояние от кромок ![]() и
и ![]() , то
боковые стенки и дно резервуара не будут влиять на степень сжатия струи. Такое
сжатие получило название совершенного сжатия.
, то
боковые стенки и дно резервуара не будут влиять на степень сжатия струи. Такое
сжатие получило название совершенного сжатия.
При
истечении воды из малых отверстий, как было установлено опытами, в случае
совершенного сжатия ![]() .
.
Несовершенное сжатие происходит при несоблюдении условия, и сжатие струи уменьшается.
Большие отверстия - отверстия, в которых давления в пределах живого сечения существенно отличаются от давления на его границах. В связи с этим скорости в разных точках различны.
Насадками
называют короткие трубы, присоединенные к стенке резервуара, если их длина ![]() (d -
диаметр отверстия).
(d -
диаметр отверстия).
6.2. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПОСТОЯННОМ НАПОРЕ
Отверстие незатопленное
Для определения скорости и расхода жидкости, вытекающей из отверстия, применяем уравнение Бернулли. Принимаем сечение 1-1 по свободной поверхности жидкости в резервуаре, второе сечение 2-2 проведем через сжатое сечение струи С-С. Плоскость сравнения 0-0 проводим через центр сжатого сечения параллельно свободной поверхности (см. рис. 6.1). Истечение жидкости осуществляется в атмосферу.
Напишем уравнение Бернулли для сечений 1-1 и 2-2:
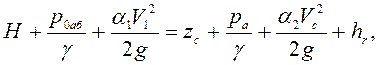 (6.2)
(6.2)
где ![]() - абсолютное давление на свободной поверхности жидкости в
резервуаре;
- абсолютное давление на свободной поверхности жидкости в
резервуаре; ![]() ,
, ![]() -
средние скорости в соответствующих сечениях;
-
средние скорости в соответствующих сечениях; ![]() ;
; ![]() - потери напора на участке от сечений 1-1
к 2-2.
- потери напора на участке от сечений 1-1
к 2-2.
Согласно формуле Вейсбаха
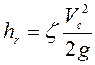 ,
,
где ![]() -
коэффициент местных сопротивлений отверстия.
-
коэффициент местных сопротивлений отверстия.
Принимаем
![]() .
.
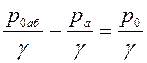 (
(![]() - избыточное давление в сечении 1-1).
- избыточное давление в сечении 1-1).
Следовательно,
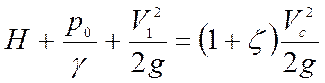 . (6.3)
. (6.3)
Скоростью
![]() , в резервуаре можно пренебречь, считая что
площадь его поперечного сечения
, в резервуаре можно пренебречь, считая что
площадь его поперечного сечения ![]() .
.
Величину
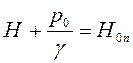 назовем
приведенным напором.
назовем
приведенным напором.
Тогда
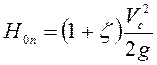 . (6.4)
. (6.4)
Отсюда скорость в сжатом сечении
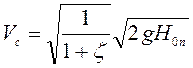 . (6.5)
. (6.5)
Введем следующее обозначение:
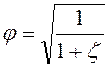 , (6.6)
, (6.6)
uде ![]() - коэффициент скорости истечения.
- коэффициент скорости истечения.
Окончательно формула скорости истечения будет иметь следующий вид:
![]() . (6.7)
. (6.7)
Для
частного случая, когда ![]() , т.е. резервуар сообщается с
атмосферой,
, т.е. резервуар сообщается с
атмосферой,
![]() .
.
В результате скорость
![]() . (6.8)
. (6.8)
Для
идеальной жидкости потери напора ![]() и
и ![]() , а коэффициент скорости
, а коэффициент скорости ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.