Истечение жидкости через отверстия и насадки, страница 5

Найдем значение вакуумметрического давления, имеющего место в сжатом сечении. Напишем уравнение Бернулли для сечений 2-2 (сжатое сечение С-С) и 3-3 на выходе из насадка. Плоскость сравнения проходит по оси насадка (см. рис. 6.9).

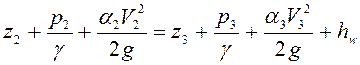,               (6.30)

где ;  - абсолютное давление, ; .

Принимаем ; ; ;  - гидравлические потери на участке от сечения 2-2 до 3-3.

Потери напора по длине принимаем .

Потери напора  приближенно определяем, как потери напора на внезапном расширении, .

После подстановок получим

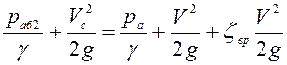.                           (6.31)

Вакуумметрический напор

.

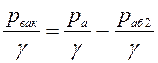Тогда согласно (6.31)

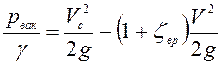.                                     (6.32)

Коэффициент внезапного расширения .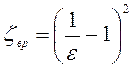

Согласно уравнению неразрывности выразим скорость в сжатом сечении через V:

,  ,

тогда

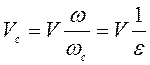,                                                 (6.33)

где  - коэффициент сжатия.

В результате вакуумметрический напор будет

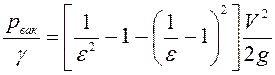.                            (6.34)

Выражение, стоящее перед скоростным напором , преобразуем к виду

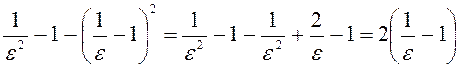.       (6.35)

Подставив (6.35) в (6.34), получим

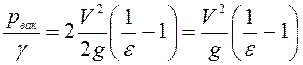                         (6.36)

Выразим скорость V через напор H:

.

Заменим в зависимости (6.36) скорость, откуда вакуумметрический напор

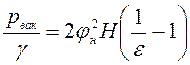.                                           (6.37)

Как уже отмечалось ранее, для внешнего цилиндрического насадка коэффициент скорости . Коэффициент сжатия струи в насадке принимаем . Согласно вышеизложенному определим вакуумметрический напор по уравнению (6.37) с учетом напора H:

.

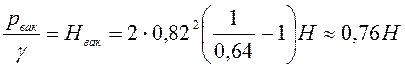Опытами было установлено, что срыв вакуума происходит, если максимальный вакуумметрический напор  м и начинается подсасывание воздуха через выходное отверстие насадка, а истечение жидкости осуществляется аналогично отверстию в тонкой стенке.

Предельное значение напора H, при котором истечение из насадка будет работать без срыва вакуума,

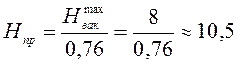 м.

Таким образом, истечение струи из внешнего цилиндрического насадка полным сечением будет происходить при  м и предельном напоре  м при длине насадка .

Внутренние цилиндрические насадки

Цилиндрический насадок, находящийся внутри резервуара, называется внутренним насадком (см. рис. 6.8). На входе в такой насадок поток (струя) претерпевает большее сжатие, чем это имеет место во внешнем насадке. Причиной этого является обтекание потоком входного отверстия насадка с относительно малой толщиной по кромке . Сопротивления на входе, связанные с деформацией потока, зависят от относительной толщины передней кромки насадка .

Установлено, если , то истечение происходит аналогично истечению из малого отверстия, т.е. струя, отрываясь от кромок, не касается стенок насадка. При  получены следующие значения коэффициентов: коэффициент скорости ; коэффициент расхода ; коэффициент сжатия . Значения коэффициентов ,  значительно меньше, чем для отверстия в тонкой стенке.

В случае увеличения длины насадка () внутренний насадок работает, как правило, полным сечением; при  имеем ; .

Нецилиндрические насадки

Конические насадки. К коническим насадкам относятся сходящиеся и расходящиеся насадки (рис. 6.10). Сходящийся насадок имеет форму усеченного конуса, образующие которого направлены к выходному отверстию. В таких насадках деформация потока достаточно мала, водоворотная вихревая область незначительна и потери напора существенно меньше, чем у цилиндрического насадка.

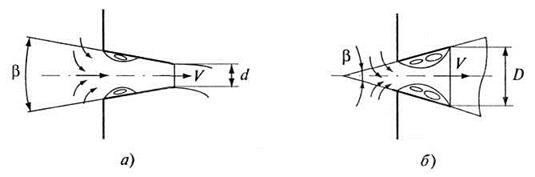
Рис. 6.10. Конические насадки: а - сходящийся (сужающий); б - расходящийся

Опытами установлено, что коэффициент расхода для конических насадков достигает максимальных значений  при угле конусности , а коэффициент сжатия на выходе . Увеличение угла  приводит к уменьшению  и увеличению сжатия струи на выходе. Для квадратных и прямоугольных форм сечения насадков угол конусности принимается , при этом коэффициент расхода .