Истечение жидкости через отверстия и насадки, страница 3

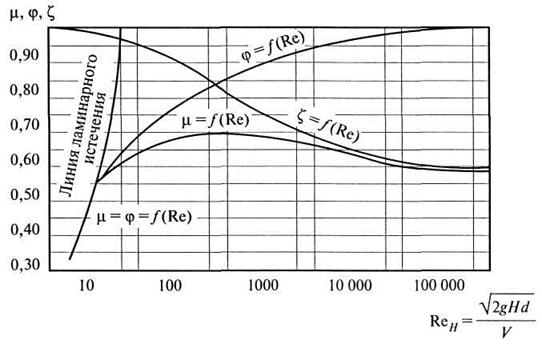
Рис. 6.3. Зависимость коэффициентов истечения из малых отверстий в тонкой стенке от числа Рейнольдса

♦ Пример 6.1

Определить длину трубопровода диаметром  мм, при котором расход вытекающей воды будет такой же, как из малого отверстия того же диаметра, если напоры воды соответственно равны  м и  м . Коэффициент гидравлического трения трубы принять равным . Температура воды  (рис. 6.4).

Формулы расхода при истечении жидкости из отверстия и трубы:

;

.

Площади поперечных сечений отверстия и трубы () равны .

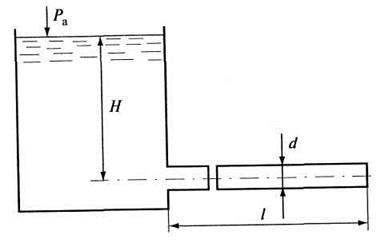
Рис. 6.4. К примерам 6.1 и 6.8

Расходы , тогда

.

Коэффициент расхода малого отверстия  найдем, используя зависимость  (см. рис. 6.3).

Определим число Рейнольдса

,

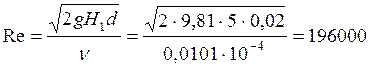м/с² при  (табл. П1.4 приложения).

По графику (см. рис. 6.3) находим для полученного Re .

Коэффициент расхода трубы

,

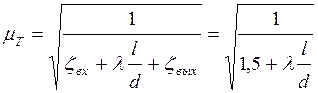;  (табл. П 1.4 приложения).

Возведем в квадрат равенство расходов, полученное ранее:

,

Откуда

;

.

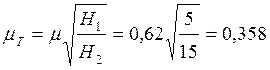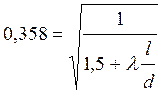Из полученного выражения находим длину трубопровода:

;

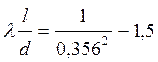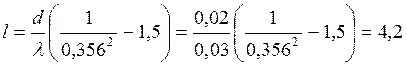 м.

Длина трубопровода  м.

♦ Пример 6.2

Два резервуара, напоры в которых поддерживаются постоянными и равными соответственно  м и  м, соединены между собой короткой трубой длиной  м. Расход воды, протекающий из одного резервуара в другой,  л/с. Температура воды . Определить диаметр трубы, приняв  (рис. 6.5).

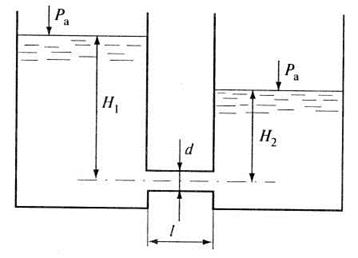
Рис. 6.5. К примеру 6.2

Напор, при котором происходит истечение воды из одного резервуара в другой,

м.

Расход воды определяется по формуле

.

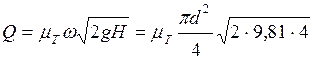Коэффициент расхода короткой трубы  при ;  (табл. П 1.5 приложения)

.

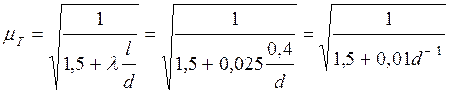Диаметр трубы находим методом подбора, задаваясь разными значениями d. Вычисления  и  сводим в табл. 6.1.

Таблица 6.1 - Результаты вычисления

№ п/п	d, м		Q, м3/с
1	0,03	0,739	0,0046
2	0,04	0,756	0,0084
3	0,05	0,767	0,0133

Диаметру d=50 мм соответствует расход Q=13,3 л/с, что удовлетворяет условию примера.

6.3. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ БОЛЬШИЕ ОТВЕРСТИЯ

Отверстия являются большими, если давление в пределах их живого сечения переменно, а скорость увеличивается по мере удаления от верхней кромки отверстия. Рассмотрим большое отверстие произвольной формы в тонкой стенке (рис. 6.6). Напор по верхней кромке отверстия , по нижней - . Выделим в большом отверстии горизонтальную полоску высотой , которую будем считать как площадь малого отверстия. Напор для такого отверстия полагаем постоянным и равным Н. Элементарный расход, проходящий через эту горизонтальную полоску,

,                                       (6.19)

где  - коэффициент расхода условного малого отверстия в виде полоски; Н - напор для малого отверстия.

Полагаем, что  для всех узких горизонтальных полосок, на которые разбивается большое отверстие.

Расход, проходящий через все горизонтальные полоски, получим, интегрируя  (6.19), а постоянные величины выносим за знак интеграла:

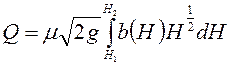.                                     (6.20)

При нахождении расхода по формуле (6.20) необходимо знать функциональную зависимость переменной ширины от высоты большого отверстия.

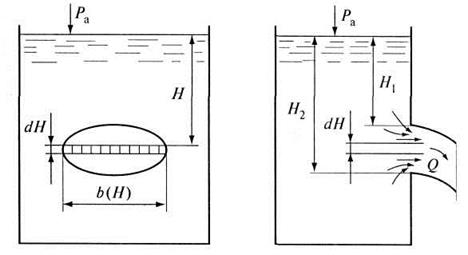
Рис. 6.6. Истечение из большого отверстия произвольной формы

Рассмотрим частный случай большого отверстия прямоугольной формы (рис. 6.7). Ширина отверстия равна . Расход жидкости для прямоугольного отверстия согласно зависимости (6.20) после интегрирования

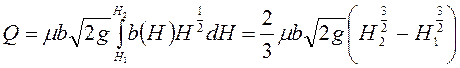.       (6.21)

Расход жидкости может быть также вычислен, принимая напор истечения относительно центра тяжести большого отверстия .

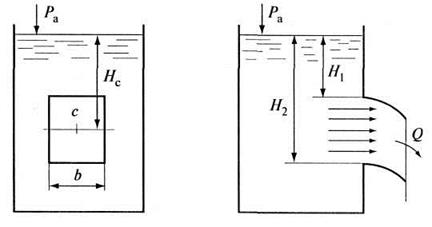
Рис. 6.7. Истечение из большого прямоугольного отверстия в тонкой стенке

 - расстояние от свободной поверхности жидкости в резервуаре до центра тяжести большого отверстия. Тогда

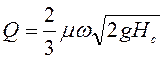                                                                        (6.22)

или

,                                                 (6.23)