Истечение жидкости через отверстия и насадки, страница 7

.

Объем жидкости за dt

.                                  (6.40)

Одновременно с понижением уровня в резервуаре на dH объем жидкости в нем уменьшится на dW:

.

Знак минус принят потому, что напор Н понижается.

Следовательно,

.                                       (6.41)

Отсюда, разделив переменные в дифференциальном уравнении (6.41), получим

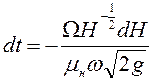.                                                 (6.42)

Проинтегрируем уравнение (6.42) в пределах от  до :

.

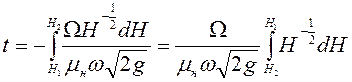Окончательно получим

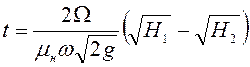.                                 (6.43)

Полное опорожнение резервуара наступит при снижении уровня жидкости до оси насадка, т.е. . Тогда время опорожнения резервуара

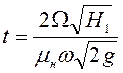.                                                                (6.44)

Объем резервуара .

Умножим и разделим уравнение (6.44) на , тогда получим

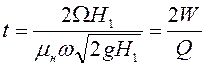.                                                  (6.45)

Знаменатель уравнения (6.45) - расход Q при напоре  Полное опорожнение резервуара при переменном напоре происходит за время, в 2 раза большее, чем истечение того же объема при постоянном напоре.

Истечение при переменном напоре в сообщающихся резервуарах

Рассмотрим два сообщающихся резервуара, соединенных между собой короткой трубой. Площади поперечных сечений резервуаров постоянны. Площадь первого равна , второго - . Жидкость из первого резервуара по короткой трубе площадью поперечного сечения  перетекает во второй, при этом уровень жидкости в одном резервуаре понижается, а в другом - увеличивается (рис. 6.14). За время t уровни в обоих резервуарах сравниваются и переток жидкости прекращается.

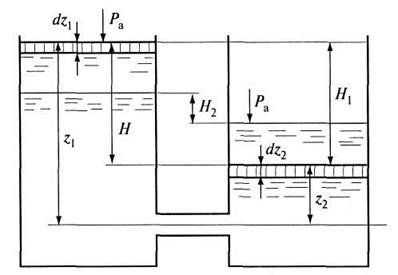
Рис. 6.14. Истечение жидкости при переменном напоре в сообщающихся резервуарах

Обозначим напоры в начальный момент времени над центром отверстия трубы в резервуарах через  и , разность напоров .

За время dt при перетоке жидкости из резервуара в резервуар уровень уменьшится на величину , в другом увеличится на .

Изменение напора за dt составит

.                                                   (6.46)

Объем жидкости в первом резервуаре уменьшится на , во втором увеличится на .

Следовательно, можно записать

,                                                 (6.47)

откуда

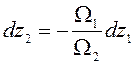.                                                                              (6.48)

Подставив  из (6.48) в (6.46), получим

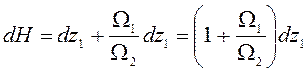                                    (6.49)

или

.

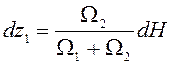За время dt при напоре Н произойдет приток жидкости объемом dW во второй резервуар. Этот объем

.                                            (6.51)

Уменьшение объема .

Следовательно,

.                                                           (6.52)

Разделим переменные, получим

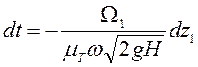.                                          (6.53)

Подставим значение  из (6.50) в (6.53), получим

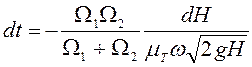.                                (6.54)

Интегрируем полученное уравнение в пределах от  до  и выносим постоянные за знак интеграла:

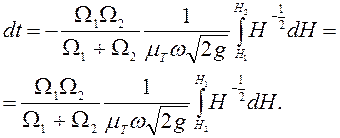
Отсюда время , за которое разность уровней изменится от от  до ,

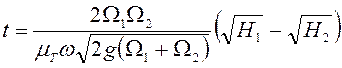.                  (6.55)

Полное выравнивание уровней жидкости в резервуарах произойдет, когда .

Время, когда уровни сравняются, вычисляется по формуле

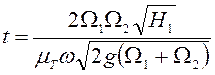.                                       (6.56)

♦ Пример 6.4

Определить время, за которое разность уровней Н в двух резервуарах уменьшится с  до . Уровень воды в правом резервуаре поддерживается постоянным. В левом цилиндрическом резервуаре диаметр  м. Резервуары соединены между собой трубой длиной  м и диаметром  мм. Эквивалентная шероховатость трубы  мм,  м,  м (рис. 6.15).

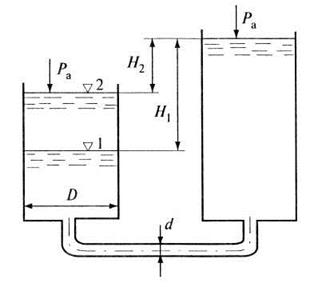
Рис. 6.15. К примеру 6.4

Время изменения уровней в резервуарах находится по формуле (6.43):

.

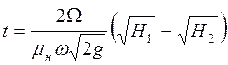Коэффициент расхода трубы ;  (табл. П.4 приложения).

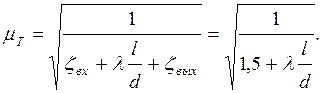
Полагаем, что движение воды в трубе соответствует квадратичной области сопротивлений. Коэффициент гидравлического трения определяем по формуле Шифринсона:

;

.

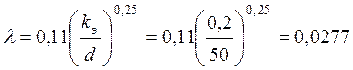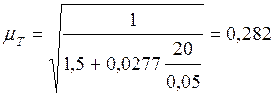Площади поперечного сечения резервуара и трубы