Истечение жидкости через отверстия и насадки, страница 2

Теоретическая скорость истечения в этом случае

.                                                         (6.9)

Зависимость (6.9) - формула Торричелли, полученная им в 1643 г. на основании опытов при определении скоростей истечения в случае разных напоров .

Физический смысл коэффициента  заключается в том, что он выражает отношение действительной скорости  к теоретической скорости  ().

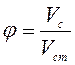Зная скорость истечения, можно найти расход Q. При условии, что ,

.                                        (6.10)

Назовем произведение двух коэффициентов  и  коэффициентом расхода отверстия :

.                                                            (6.11)

Тогда выражение для расхода при истечении через отверстие будет

.                                                    (6.12)

Коэффициент расхода учитывает как степень сжатия, так и потери напора , характеризующиеся коэффициентом местных сопротивлений .

Коэффициент  определяется опытным путем, и его значение изменяется в диапазоне 0,590,64. Как правило, для предварительных расчетов принимается .

Следует отметить, что при истечении через малые отверстия за сжатым сечением происходит деформация поперечного сечения струи. Форма деформированного сечения отличается от формы сечения отверстия, из которого происходит истечение. Такое явление носит название инверсии струи, которая происходит из-за поверхностного натяжения жидкости. Например, при истечении из круглого отверстия поперечное сечение струи имеет форму эллипса, а для квадратного сечения струя приобретает крестообразную форму.

Отверстие затопленное

Рассматриваем малое отверстие в тонкой стенке, из которого происходит истечение под уровень жидкости (рис. 6.2). Давления на свободные поверхности жидкости в резервуарах равны атмосферному . Поверхности уровней как в правом, так и в левом резервуаре не изменяют своего положения за определенное время.

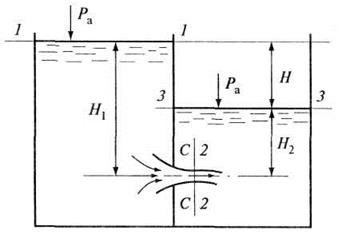
Рис. 6.2. Истечение под уровень жидкости

Напишем уравнение Бернулли для сечений 1-1 и 3-3 относительно плоскости сравнения, проходящей через центр отверстия параллельно свободным поверхностям в резервуарах:

;

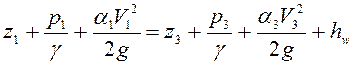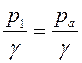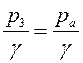; ; ;                   (6.13)

Пренебрегаем величинами  и 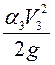 вследствие их малости, так как площади поперечных сечений резервуаров  и  ( - площадь малого отверстия). После подстановок получим

,                                                     (6.14)

где ;  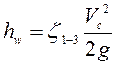- гидравлические потери напора;  - коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 3-3;  - средняя скорость течения в сжатом сечении С-С (2-2).

Потери напора между выбранными сечениями состоят из потерь при истечении из отверстия, т.е. от сечения 1-1 до 2-2 (С-С) и от сечения 2-2 до сечения 3-3, где происходит внезапное расширение струи до существенно больших размеров:

                                                     (6.15)

Потери при истечении из отверстия

.

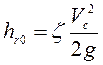Потери при внезапном расширении струи определяем по формуле Борда (4.126):

,

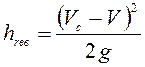где  - скорость в резервуаре при расширении струи, .

Потери напора будут

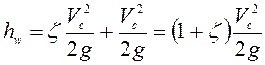.                              (6.16)

Скорость в сжатом сечении

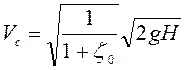                                             (6.17)

или

.

Формула расхода для сжатого сечения при истечении через затопленное отверстие:

.                    (6.18)

Полученная формула расхода аналогична формуле расхода для незатопленного отверстия. Различие формул заключается в том, что напор истечения Н выражает разность уровней  жидкости в резервуарах.

Установлено при проведении многочисленных опытов, что значения ,  для затопленного и незатопленного отверстий практически одинаковы. Поэтому в случае определения расхода или скорости через затопленное отверстие коэффициенты принимаются такими же, как и для незатопленного отверстия. На основании опытов разных авторов А. Альтшулем был создан график для малых круглых отверстий коэффициентов , ,  в зависимости от числа Рейнольдса (рис. 6.3). Для квадратичной области сопротивления при турбулентном режиме, т.е. при больших числах 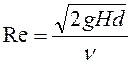, принимаются ; ; ; .