




МОиН РФ
Новосибирский Государственный Технический Университет
по Вычислительной математике
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Выполнили: Преподаватель:
Ильин М.Э. Чикильдин Г.П.
Аникин А.С.
Кайгородов Ю.В.
Новосибирск, 2004
Цель работы:
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
Постановка задачи:
Решить систему
линейных алгебраических уравнений (СЛАУ) Ax=b, ![]() ,
, ![]()
![]() итерационными методами Зейделя и наискорейшего
спуска с точностью
итерационными методами Зейделя и наискорейшего
спуска с точностью ![]() .
Для сравнения с истинными значениями корней выполнить решение САУ методом
Гаусса.
.
Для сравнения с истинными значениями корней выполнить решение САУ методом
Гаусса.
Алгоритмы в общем виде:
Ax=b, ![]() ,
, ![]()
![]()
Метод
Зейделя:![]() xi[0]=xi0 , i
xi[0]=xi0 , i![]() [1,n],
[1,n],
Xi [k+1]={bi- 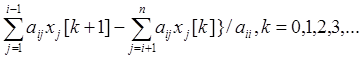 , где
, где ![]() - i-я компонента вектора x на k-й итерации, xi0,
i
- i-я компонента вектора x на k-й итерации, xi0,
i![]() [1,n]-
начальные условия, которые рекомендуется задавить в виде xi [0]=
[1,n]-
начальные условия, которые рекомендуется задавить в виде xi [0]=![]() , i
, i![]() [1,n].
[1,n].
Метод Зейделя будет сходится к единственному решению при выполнении условия
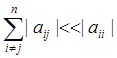 , , i
, , i![]() [1,n], , j
[1,n], , j![]() [1,n].
[1,n].
xi[0]=xi0 , i![]() [1,n], xi
[k+1]= xi [k]+αi [k] gi [k],
k=0,1,2,...,
[1,n], xi
[k+1]= xi [k]+αi [k] gi [k],
k=0,1,2,...,
gi [k]=bi- 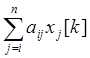 , α[k]=
, α[k]=![]() ,
d[k]=
,
d[k]= 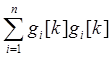 ,
c[k]=
,
c[k]= 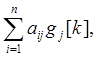 где
где
![]() - i-я компонента
вектора x на k-й итерации, xi0, i
- i-я компонента
вектора x на k-й итерации, xi0, i![]() [1,n]-
начальные условия, которые рекомендуется задавить в виде xi [0]=0, i
[1,n]-
начальные условия, которые рекомендуется задавить в виде xi [0]=0, i![]() [1,n].
[1,n].
Метод наискорейшего спуска сходится к единственному решению, если матрица А – симметрическая, положительно определенная.
В общем случае для неособенной матрицы А можно предусмотреть условие сходимости метода путем первой трансформации Гаусса исходной САУ
ATAx=ATb, где матрица ATA – симметрическая, положительно определенная.
Листинг 1. Программа
integer i,n,k,k1
real a(5,5),b(5),e,g(5),x(5),summ, x2(5),x3(5), xbet(5)
real summbet, gbet(5), max2, max3, a2(5,5)
real at(5,5), u(5,5), v(5)
data a /0.380, 0.052, 0.030, 0.060, 0.250,
* -0.050, 0.595, 0.000, 0.126, 0.000,
* 0.010, 0.000, 0.478, 0.000, 0.090,
* 0.020, -0.040, -0.140, 0.470, 0.010,
* 0.070, 0.040, 0.080, -0.020, 0.560/
data b /-2.140, 1.833, 1.736, -1.242, 1.440/
data x /0,0,0,0,0/
e=0.0001
n=5
summ=0
summbet=0
k1=0
data g /0,0,0,0,0/
data gbet /0,0,0,0,0/
do 110 i=1,5
110 xbet(i)=b(i)/a(i,i)
call n1ygau(a,b,x3,n)
write (5,40) k, x3(1),x3(2), x3(3),x3(4), x3(5)
do 100 k=0,15
102 write (2,40) k1, x(1), x(2), x(3), x(4), x(5)
write (3,40) k1, g(1), g(2), g(3), g(4), g(5)
write (8, 41) k1, x3(1), x(1), xbet(1)
41 format (i4, 2x, f11.4, 2x, f11.4, 2x, f11.4)
write (7,49) max2
write (21,40) k1, xbet(1), xbet(2), xbet(3), xbet(4), xbet(5)
write (4,40) k1, x2(1), x2(2), x2(3), x2(4), x2(5)
40 format (i4, 2x, f11.4,2x,f11.4,2x,f11.4, 2x,f11.4,2x,f11.4)
call n1ymgs(a,b,n,gbet,xbet)
call n1ymgs(a,b,n,g,x)
call n1ymns(a,b,n,g,x2)
do 200 i=1,n
summ=0.0
summbet=0.0
do 300 j=1,n
summ=summ+a(i,j)*x(j)
300 summbet=summbet+a(i,j)*xbet(j)
g(i)=b(i)-summ
200 gbet(i)=b(i)-summbet
call findmax(g,n,max2)
max2=abs(max2)
49 format (5x, f9.4)
k1=k1+1
if (max2.le.e) GOTO 101
GOTO 102
100 continue
101 do 201 i=1,5
do 202 j=1,5
202 a2(i,j)=a(i,j)
201 n=n
call n1ytga(a2,b,n,at,u,v)
do 301 i=1,5
write (19,6) (u(i,j), j=1,5)
301 n=n
6 format (5(1x, f9.5))
C write (8,7) (v(i), i=1,5)
7 format (2x, 5(2x,f9.5))
stop
end
integer i,n,k,k1
real a(5,5),b(5),e,g(5),x(5),summ, x2(5),x3(5), xbet(5)
real summbet, gbet(5), max2, max3, a2(5,5)
real at(5,5), u(5,5), v(5)
data a /0.380, 0.052, 0.030, 0.060, 0.250,
* -0.050, 0.595, 0.000, 0.126, 0.000,
* 0.010, 0.000, 0.478, 0.000, 0.090,
* 0.020, -0.040, -0.140, 0.470, 0.010,
* 0.070, 0.040, 0.080, -0.020, 0.560/
data b /-2.140, 1.833, 1.736, -1.242, 1.440/
data x /0,0,0,0,0/
e=0.0001
n=5
summ=0
summbet=0
k1=0
data g /0,0,0,0,0/
data gbet /0,0,0,0,0/
do 110 i=1,5
110 xbet(i)=b(i)/a(i,i)
call n1ygau(a,b,x3,n)
write (5,40) k, x3(1),x3(2), x3(3),x3(4), x3(5)
do 100 k=0,15
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.