Математика \ Вычислительная математика

Решение системы линейных алгебраических уравнений, страница 2

  102 write (2,40) k1, x(1), x(2), x(3), x(4), x(5)

      write (3,40) k1, g(1), g(2), g(3), g(4), g(5)

      write (8, 41) k1, x3(1), x(1), xbet(1)

   41 format (i4, 2x, f11.4, 2x, f11.4, 2x, f11.4)

      write (7,49) max2

      write (21,40) k1, xbet(1), xbet(2), xbet(3), xbet(4), xbet(5)

      write (4,40) k1, x2(1), x2(2), x2(3), x2(4), x2(5)

   40 format (i4, 2x, f11.4,2x,f11.4,2x,f11.4, 2x,f11.4,2x,f11.4)

      call n1ymgs(a,b,n,gbet,xbet)

      call n1ymgs(a,b,n,g,x)

      call n1ymns(a,b,n,g,x2)

      do 200 i=1,n

      summ=0.0

      summbet=0.0

      do 300 j=1,n

      summ=summ+a(i,j)*x(j)

  300 summbet=summbet+a(i,j)*xbet(j)

      g(i)=b(i)-summ

  200 gbet(i)=b(i)-summbet

      call findmax(g,n,max2)

      max2=abs(max2)

   49 format (5x, f9.4)

      k1=k1+1

      if (max2.le.e) GOTO 101

      GOTO 102

  100 continue

  101 do 201 i=1,5

      do 202 j=1,5

  202 a2(i,j)=a(i,j)

  201 n=n

      call n1ytga(a2,b,n,at,u,v)

      do 301 i=1,5

      write (19,6) (u(i,j), j=1,5)

  301 n=n

    6 format (5(1x, f9.5))

C     write (8,7) (v(i), i=1,5)

    7 format (2x, 5(2x,f9.5))

      stop

      end

Findmax.for

      subroutine findmax(c,n,max)

      dimension c(n)

      integer i

      real max

      max=-10.00

      do 1 i=1,n

    1 if (c(i).gt.max) max=c(i)

      return

      end

Листинг 2. Файл результата

С  нулевыми нач.условиями(Зейдель)

   k       x(1)         x(2)         x(3)         x(4)         x(5)

   0       0.0000       0.0000       0.0000       0.0000       0.0000

   1      -5.6316       3.5322       3.9625      -2.8825       4.9279

   2      -6.0271       3.0875       2.3421      -2.4930       4.9279

   3      -6.0635       3.1114       2.4574      -2.4930       4.9279

табл.1

С ненулевыми нач.условиями(Зейдель)

   k      x(1)          x(2)         x(3)        x(4)          x(5)

   0      -5.6316       3.0807       3.6318      -2.6426       2.5714

   1      -5.6564       3.2229       2.7799      -2.6793       4.9279

   2      -6.0474       3.0992       2.4023      -2.4930       4.9279

   3      -6.0636       3.1116       2.4574      -2.4930       4.9279

табл.2

Метод наименьшего спуска

   k      x(1)          x(2)         x(3)        x(4)          x(5)

   0       0.0000       0.0000       0.0000       0.0000       0.0000

   1      -3.9770       3.9507       3.5143      -2.5498       4.5898

   2      -5.7018       2.7901       2.3734      -2.5163       4.9865

   3      -5.9951       3.1480       2.4343      -2.4913       4.9313

   4      -6.0478       3.1002       2.4583      -2.4928       4.9275

   5      -6.0602       3.1134       2.4576      -2.4930       4.9278

   6      -6.0626       3.1112       2.4574      -2.4930       4.9279

   7      -6.0632       3.1118       2.4574      -2.4930       4.9279

   8      -6.0633       3.1117       2.4574      -2.4930       4.9279

   9      -6.0634       3.1117       2.4574      -2.4930       4.9279

табл.3

Метод Гаусса

   k      x(1)          x(2)         x(3)        x(4)          x(5)

   0      -6.0634       3.1117       2.4574      -2.4930       4.9279

табл.4

Табличка сходимости (рис. 1)

   0      -6.0634       -5.6316        0.0000 

   1      -6.0634       -5.6564       -5.6316 

   2      -6.0634       -6.0474       -6.0271 

   3      -6.0634       -6.0636       -6.0635 

табл.5

Табличка сходимости (рис. 2)

   K       Гаусс        Зейдель     Наискор спуск

   0      -6.0634       0.0000       0.0000

   1      -6.0634      -5.6316      -3.9770

   2      -6.0634      -6.0271      -5.7018

   3      -6.0634      -6.0635      -5.9951

   4      -6.0634      -6.0634      -6.0478

   5      -6.0634      -6.0634      -6.0602

   6      -6.0634      -6.0634      -6.0626

   7      -6.0634      -6.0634      -6.0632

   8      -6.0634      -6.0634      -6.0633

   9      -6.0634      -6.0634      -6.0634

табл.6

График сходимости  методов итерации

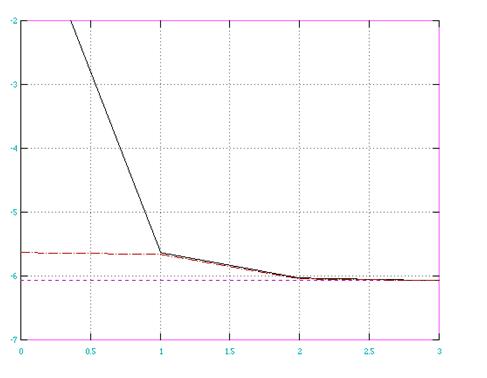
рис. 1 Метод  Зейделя (красная пунктирная),  наискорейшего спуска (коричневая сплошная)

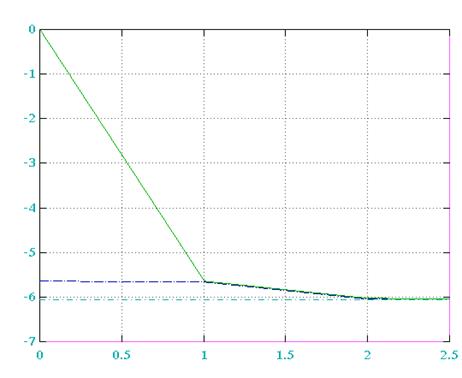
рис. 2 График сходимости метода Зейделя при различных начальных условиях (сплошная – нулевые нач. условия, штрихпунктирная – ненулевые нач. условия)

Вывод: В результате проделанной лабораторной работы,  мы получили практический опыт работы с итерационными алгоритмами вычисления решения САУ. Мы использовали метод Зейделя и наискорейшего спуска и выяснили, что метод Зейделя более эффективен, чем метод наискорейшего спуска, т.к. метод Зейделя приближается к истинному результату за меньшее число итераций.

Скачать файл