Интерполирование функций. Интерполяционный полином Лагранжа

[4]. Интерполирование функций. Интерполяционный полином Лагранжа.

 ПРИБЛИЖЕНИЕ ФУНКЦИИ

При решении ряда практических задач возникает необходимость замены одной функции другой, более простой, но достаточно близкой к первой. Данный подход может иметь место, например, при много­кратных вычислениях на ЭВМ функции, заданной громоздким аналити­ческим выражением или при вычислении интегралов, которые невозмож­но взять по таблицам. В других задачах, особенно при обработке экспериментальных данных, получаемых в ходе различных исследова­ний, требуется синтезировать математическую модель функции, пред­ставленной в табличном виде. Эти задачи могут быть решены методами теории приближения функций, среди которых в данном разделе рас­сматриваются интерполирование, приближение сплайнами, наилучшее равномерное приближение и среднеквадратичная аппроксимация.

Интерполирование функций

Пусть на интервале [a, b] заданы (п + 1) точка  и соответствующие им значения  функции у = f(x), принадлежащей пространст­ву непрерывных и дифференцируемых функций. Другими словами, f(x) представлена в виде таблицы  

Требуется определить некоторую F(х), которая бы обеспечивала  и посредством которой можно бы­ло бы приближенно вычислить f(x) для . Данный способ определения f(x) для любого х  называет­ся интерполированием  f(x), а точки  - узлами, интер­поляции. Но в такой постановке задача интерполирования является некорректной, поскольку через систему точек  графически можно провести бесчисленное множество кривых, каждая из которых будет соответствовать своей F(х). Регуляризация задачи осуществляется за счет ограничения класса функций F(х), которые выбираются в виде полиномов и решение будет единственным, если за­дать степень п полинома. Таким образом, F(х) ищется в виде

(1.1)

а коэффициенты  могут быть определены из условия .

Действительно, полагая в можно сформировать систему линейных алгебраических уравнений

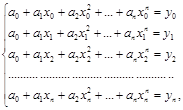
которая имеет единственное решение, поскольку ее определитель

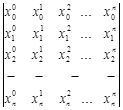
весьма специфичен, известен в математике как определитель Вандермонда и он всегда отличен от нуля [1].

Таким образом, интерполяционный полином Р (х) для функции f(x) существует, и он единственный.

Описанный способ определения коэффициентов  по­линома (1.1) может использоваться при решении практических задач интерполирования. Однако существуют другие, более простые методы вычисления .

                                        Полином Лагранжа

Интерполяционный полином будем отыскивать в виде

  - многочлены степени n, для которых узлы  являются корнями, а  т.е.

            (1.3)

Имея в виду условие (1.3), многочлены l_i(x) можно записать следую­щим образом:

(1.4)- коэффициенты, которые могут быть найдены, если положить . Тогда с учетом l_i(x_i) = 1 получаем

Подставляя  (1.5) в (1.4), a  (1.4) в (1.2), окончательно имеем

или в компактной форме

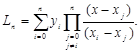               (1.6)

Выражение (1.6) представляет собой интерполяционный полином Лагранжа, который может использоваться в наиболее общем случае реше­ния задачи интерполирования.

Существует другая форма записи полинома Лагранжа. Введем обозначение

  (1.7)

Производная  будет иметь вид

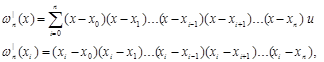а формула интерполяционного полинома Лагранжа запишется как

             (1.8)