Значение координаты x1, при котором имеет место минимум
целевой функции, обозначим как. На следующем шаге зафиксируем значения
координат
и отыщем
который будет иметь место при
В результате после n шагов получим
и, таким образом, после одной итерации
покоординатного спуска осуществляется переход из точки
и(x0) в точку
и(x1). На следующей итерации описанная шаговая процедура
покоординатного спуска повторяется и так до тех пор, пока на некоторой k-й
итерации для задаваемой точности ℰ не
выполнится, например, условие
В методе покоординатного спуска решение задачи
многомерной оптимизации сводится к поиску экстремума функции одной переменной
и, следовательно, основным моментом является выбор алгоритма одномерной
оптимизации, в качестве которого может быть использован, например, метод
золотого сечения.
Метод наискорейшего
градиентного спуска.
Из математики известно, что направление наибольшего возрастания функции
нескольких переменных характеризуется ее вектором градиента
Следовательно, вычислив для
некоторого
и осуществляя движение в сторону
противоположную направлению вектора градиента будем обеспечивать уменьшение
целевой функции. На этом принципе и базируются градиентные методы, что можно
представить в виде
где h - шаг
спуска, x0 - начальное приближение к точке
минимума. Если в выражении (6.2) шаг спуска h
=const, то данная
итерационная процедура представляет собой м
етод градиентного спуска.
Останов итерационного процесса (6.2) осуществляется при выполнении, например,
условия
Недостатком метода градиентного спуска
является ого сложность реализации, поскольку на каждом k-м шаге оптимизации необходимо вычислять частные производные
целевой функции, что особенно затруднительно, если u(x) представлена не
в аналитическом виде.
Более свободен от указанного
недостатка
лзтод жшснореОшего градиентного спуска, отличающийся тем, что
в выражении (6.2) величина h≠const, а движение из точки
осуществляется до тех пор, пока
целевая функция убывает, достигая минимума вдоль этого направления, и только
потом вновь вычисляется вектор градиента, чтобы изменить направление движения.
Таким образом, в данном методе спуск осуществляется более крупными шагами и
градиент целевой функции вычисляется в меньшем количестве точек. Величина шага h на некоторой k-й итерации может последовательно изменяться до тех пор,
пока не будет найдено минимальное значение u(x) вдоль данного
направления, что требует неоднократного вычисления
и(х), либо параметр h может быть выбран из условия
что сводится
к минимизации данной функции по одной переменной h. Во втором
варианте выбора h отпадает необходимость неоднократного вычисления
целевой функции, однако приходится решать задачу одномерной оптимизации
функции
Метод Нелдера-Мида по сравнению с градиентными методами
оказывается значительно более простым в реализации, является очень надежным и
при n≤6 одним из самых эффективных [20].
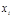 Данный метод представляет собой шаговую процедуру, на каждом k-м (k=О,1,2,...)
шаге которой в n-мерном пространстве искомых
параметров , iÎ[1, п1 формируется неправильный симплекс (выпуклый
произвольный многогранник с (n+1)-й
вершиной), определяемый своим вектором параметров
Данный метод представляет собой шаговую процедуру, на каждом k-м (k=О,1,2,...)
шаге которой в n-мерном пространстве искомых
параметров , iÎ[1, п1 формируется неправильный симплекс (выпуклый
произвольный многогранник с (n+1)-й
вершиной), определяемый своим вектором параметров
Начальный симплекс,
характеризуемый координатами
может быть выбран произвольным [20], хотя его
размеры и ориентация заметно влияют на скорость сходимости. Определение координат
вершин начального симплекса можно осуществлять по задаваемым параметрам первой
точки
и затем вычислять соответствующие
значения целевой функции
![]() Данный метод представляет собой шаговую процедуру, на каждом k-м (k=О,1,2,...)
шаге которой в n-мерном пространстве искомых
параметров , iÎ[1, п1 формируется неправильный симплекс (выпуклый
произвольный многогранник с (n+1)-й
вершиной), определяемый своим вектором параметров
Данный метод представляет собой шаговую процедуру, на каждом k-м (k=О,1,2,...)
шаге которой в n-мерном пространстве искомых
параметров , iÎ[1, п1 формируется неправильный симплекс (выпуклый
произвольный многогранник с (n+1)-й
вершиной), определяемый своим вектором параметров