МО РФ
Новосибирский Государственный Технический Университет
по Вычислительной математике
Численное Интегрирование
Выполнили: Преподаватель:
Ильин М.Э. Чикильдин Г.П.
Аникин А.С.
Кайгородов Ю.В.
Новосибирск 2004
Цель работы:
Ознакомится с квадратурными формулами Ньютона-Котеса численного интегрирования, влияние порядка точности квадратурной формулы и шага интегрирования на точность вычисления определенного интеграла.
Постановка задачи:
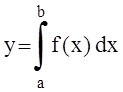, а=0, b=8
f(x)=2,0+ x1/2 *sin(x)
от функции f(x) заданной на [a,b] с шагом (Dх = 0.1, 0.2, 0.4) по средствам квадратурных формул:
m=0 формула прямоугольников(левых прямоугольников)
m=1 формула трапеций (Ньютона-Котеса 1го порядка точности)
m=2 формула парабол (Ньютона-Котеса 2го порядка точности)
m=3 формула «трех восьмых» (Ньютона-Котеса 3го порядка точности)
m=4 формула Ньютона-Котеса 4го порядка точности
Исследовать влияние шага дискретизации Dх функции f(x) на точность вычисления интеграла.
При вычислении погрешностей интегрирования e=ôyT -yô за точное значение интеграла yT следует принять его значение вычисленное с минимальным шагом Dх и максимальным порядком точности m квадратурной формулы.
Квадратурные формулы для m=0,1,2
M=0
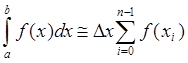
M=1
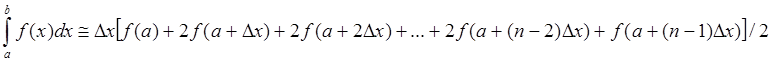
M=2
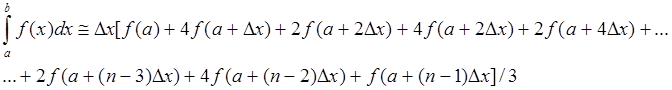
Листинг 1.
integer i,a,b,n,j,m,m1,i1,i2
real fx,dx,n1, f1(100),p,f,eee(30),dx1
a=0
b=8
write (*, 5)
5 format (3x,'Vvedite dx - shag diskretizacii',/)
read *,dx
write (*, 6)
6 format (3x,'Vvedite m - poryadok tochnosti',/)
read *,m
m1=m+1
n1=(b-a)/dx
write (*,20) n1
do 1 j=1,n1
p=a+j*dx
call func(p,fx)
f1(j)=fx
1 n=n1+1
call n1yink (f1,n,dx,m1,f)
write (2,*) ' k x F(X) '
do 2 k=1,n1
xi=a+k*dx
call func(xi,fx)
write(2, 1000) k, xi, fx
2 n1=n1
write (*,20) f
100 format (/,3x, (f9.6))
1000 format (3x, i3, 3x, f9.6, 3x, f9.6)
10 format (/,5x,i5)
20 format (/,5x,f9.6)
dx1=0.1
m1=5
call n1yink (f1,n,dx,m1,f)
yt=f
write (2, *) 'M E(dX=0.1) E(dX=0.2) E(dX=0.4)'
dx1=0.1
do 11 i1=1,5
do 12 i2=0,2
dx1=0.1*(2**i2)
m1=i1
call n1yink (f1,n,dx1,m1,f)
yi=f
eee(i2+1)=abs(yt-yi)
12 m1=m1
write (2, 400) i1, eee(1),eee(2),eee(3)
11 m1=m1
write (2, *) 'Dx E(M=1) E(M=2) E(M=3) E(M=4) E(M=5)'
dx1=0.1
do 14 i1=0,2
do 13 i2=1,5
dx1=0.1*(2**i1)
m1=i2
call n1yink (f1,n,dx1,m1,f)
yi=f
eee(i2)=abs(yt-yi)
13 m1=m1
write (2, 500) dx1, eee(1),eee(2),eee(3), eee(4), eee(5)
14 m1=m1
400 format (3x, i4, 3x, e11.6, 2x, e11.6, 2x, f8.4)
500 format (3x, f3.1,3x, 5(e11.4, 2x))
stop
end
Листинг 2. Файл результата.
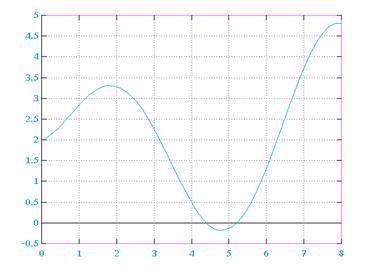
k x F(X)
1 0.100000 2.031570
2 0.200000 2.088848
3 0.300000 2.161863
4 0.400000 2.246290
5 0.500000 2.339005
6 0.600000 2.437370
7 0.700000 2.538991
8 0.800000 2.641623
9 0.900000 2.743129
10 1.000000 2.841471
11 1.100000 2.934706
12 1.200000 3.020998
13 1.300000 3.098625
14 1.400000 3.166000
15 1.500000 3.221677
16 1.600000 3.264372
17 1.700000 3.292973
18 1.800000 3.306554
19 1.900000 3.304385
20 2.000000 3.285941
21 2.100000 3.250909
22 2.200000 3.199194
23 2.300000 3.130918
24 2.400000 3.046423
25 2.500000 2.946268
26 2.600000 2.831221
27 2.700000 2.702257
28 2.800000 2.560543
29 2.900000 2.407427
30 3.000000 2.244427
31 3.100000 2.073210
32 3.200000 1.895577
33 3.300000 1.713441
34 3.400000 1.528805
35 3.500000 1.343745
36 3.600000 1.160376
37 3.700000 0.980840
38 3.800000 0.807270
39 3.900000 0.641770
40 4.000000 0.486395
41 4.100000 0.343115
42 4.200000 0.213801
43 4.300000 0.100198
44 4.400000 0.003903
45 4.500000 -0.073654
46 4.600000 -0.131230
47 4.700000 -0.167782
48 4.800000 -0.182487
49 4.900000 -0.174752
50 5.000000 -0.144220
51 5.100000 -0.090784
52 5.200000 -0.014586
53 5.300000 0.083977
54 5.400000 0.204258
55 5.500000 0.345361
56 5.600000 0.506150
57 5.700000 0.685257
58 5.800000 0.881090
59 5.900000 1.091857
60 6.000000 1.315575
61 6.100000 1.550092
62 6.200000 1.793110
63 6.300000 2.042203
64 6.400000 2.294849
65 6.500000 2.548450
66 6.600000 2.800364
67 6.700000 3.047929
68 6.800000 3.288491
69 6.900000 3.519437
70 7.000000 3.738223
71 7.100000 3.942398
72 7.200000 4.129635
73 7.300000 4.297754
74 7.400000 4.444751
75 7.500000 4.568819
76 7.600000 4.668370
77 7.700000 4.742055
78 7.800000 4.788780
79 7.900000 4.807718
80 8.000000 4.798327
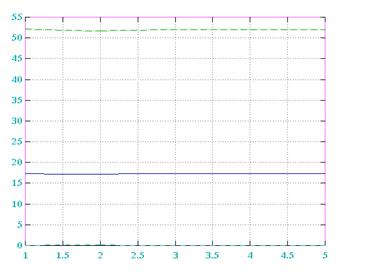
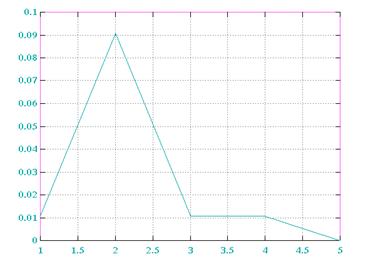
M E(dX=0.1) E(dX=0.2) E(dX=0.4)
1 .108280E-01 .173632E+02 52.0681
2 .907516E-01 .171601E+02 51.6618
3 .105724E-01 .173204E+02 51.9825
4 .105686E-01 .173205E+02 51.9825
5 .000000E+00 .173416E+02 52.0248
Dx E(M=1) E(M=2) E(M=3) E(M=4) E(M=5)
0.1 0.1083E-01 0.9075E-01 0.1057E-01 0.1057E-01 0.0000E+00
0.2 0.1736E+02 0.1716E+02 0.1732E+02 0.1732E+02 0.1734E+02
0.4 0.5207E+02 0.5166E+02 0.5198E+02 0.5198E+02 0.5202E+02
Графики функций.
y=f(x)
e=f(m) dx=0.1
dx=0.2 dx=0.4
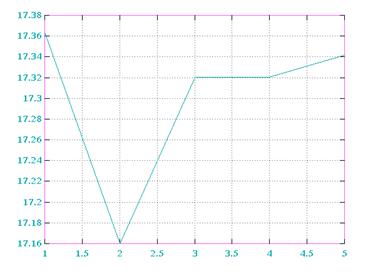
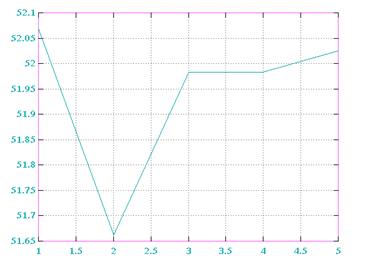
e=f(∆x) E(M=1)
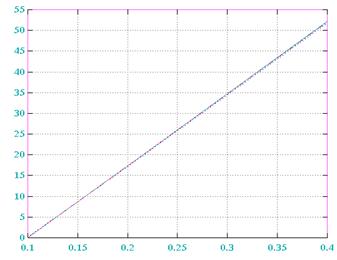
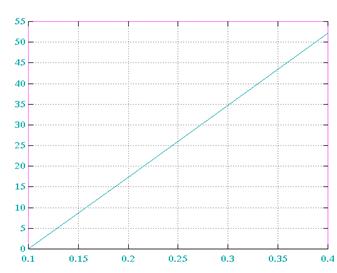
E(M=2) E(M=3)
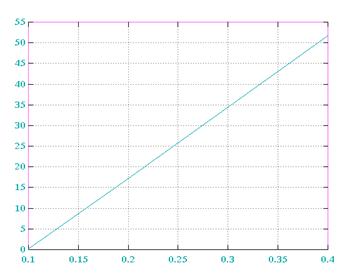
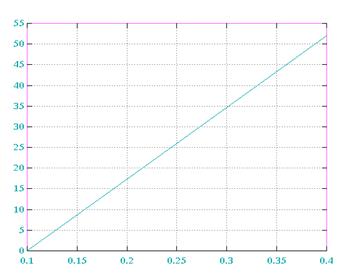
E(M=4) E(M=5)
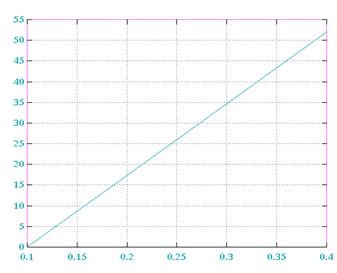
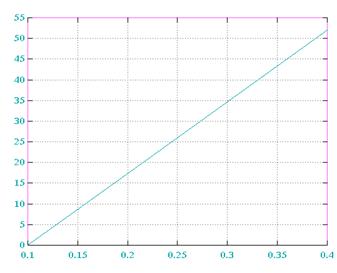
Вывод:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
