Циклический алгоритм исследования. Типы измерений и характер ошибок в них. Обработка и анализ экспериментальных данных, страница 8

Обычно для получения доверительной оценки истинного значения измеряемой величины рассчитывают ширину доверительного интервала Δ при заданной надежности  γ  (довери-тельной  вероятности).          

 Как это делается?

Ширина доверительного интервала Δ это и есть ни что иное как суммарная погрешность измерения D_S, которая, как уже обсуждалось ранее, чаще всего состоит из двух погрешностей: систематической D_С и случайной D_СЛ. Рассмотрим расчет D_S для случаев прямых и косвенных измерений.

I.  Расчет D_S для прямого измерения

1.1 Расчет систематической ошибки D_С для прямого измерения

При суммировании всех составляющих систематической погрешности (δ_і) они рассматриваются как случайные величины. Если данные о виде их функции распределения отсутствуют, то их принимают за равномерные, при которых вероятность появления данной величины постоянна на всем интервале значений. Поэтому суммарную систематическую ошибку рассчитывают по формуле:

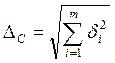
В простейшем случае, когда учитывается только одна погрешность средств измерений δ_ср.изм :

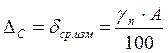
g_n – приведенная погрешность прибора (класс точности);

А – верхний предел измерения прибора.

   1.2 Расчет D_СЛ для прямого измерения

Случайная ошибка D_СЛ рассчитывается как ошибка выборки из n измерений по формуле, которая упоминалась уже ранее:

.

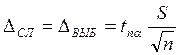Т.о., чтобы определить случайную ошибку нам нужно для заданной надежности a найти коэффициент t_na (по специальным таблицам t–распределения Стьюдента) и по результатам n измерений рассчитать среднеквадратическое отклонение S по известной формуле:

.

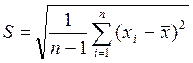После того как  систематическая и случайная ошибки определены, необходимо произвести их сравнение. Если D_С и D_СЛ сопоставимы, т.е. отличаются не более чем на порядок, то D_S определяется как сумма D_С и D_СЛ. Если D_С << D_СЛ или наоборот, то несущественной величиной пренебрегают, и вместо D_S записывают одну из погрешностей (существенную величину).

Примечание: значения D_СЛ и D_С необходимо определять при одном и том же значении вероятности.

II.      Расчет D_S для косвенного измерения

Для косвенных измерений принимается приближение D²_S = Д(y), т.е. D²_S равна дисперсии функции y = f(x). Как отмечалось ранее, дисперсии функций случайных величин рассчитываются по формуле:

.

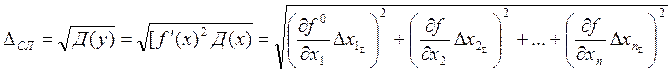Где  - суммарные погрешности прямых измерений вычисляемые по п.1.1 – 1.2 и включающие как случайную так и систематическую составляющие.

Определение суммарной погрешности для прямых и косвенных измерений можно рассматреть на примере расчета электрического сопротивления R (Ом), измеряя ток (I, A) и напряжение (U, В) (см. таблицу).

                                                                                                             Таблица

Расчет суммарной погрешности для прямого и косвенного измерения

Фактор хi		Номер опыта j				Ошибка D
Значе ние откли ка Y		1	2	…	n	Случайная	Систематическая	Суммарная
Прямые измерения	X1	X11	X12	…	X1n	Dx1сл	Dx1с	Dx1S
	(I, A)
	X2	X21	X22	...	X2n	Dx2сл	Dx2с	Dx2S
	(U, B)
	...	...	...	...	...	…	…	...
	Xm	Xm1	Xm2	...	xmn	Dxmсл	Dxmс	DxmS
Косвенные	Y	Y1	Y2	...	Yn	–	–
	(R, Ом) R = U / I

Окончательно результат измерения или истинное значение измеряемой величины В представляется в виде:

, вероятность Р = g.

В общем случае В – символ примеряемой величины,  - ее точечная оценка (результат измерения вычисленный по формуле), D = D_S - суммарная погрешность.

Примечания:

(1) Формулы для расчета теоретического среднего  и ошибки выборки D_СЛ даны для нормального закона распределения; (2) границы погрешностей записывают не более чем с двумя значащими цифрами; (3) округляют границы погрешностей всегда в большую сторону. Например, если D = 0,837, то результат пишут как а = 2,54 ± 0,84.