Циклический алгоритм исследования. Типы измерений и характер ошибок в них. Обработка и анализ экспериментальных данных, страница 6

(а)                                                       (б)

Плосковершинные распределения имеют отрицательный эксцесс (рис.б). При m₄=-2 кривые распространяются на две самостоятельные.

Непосредственно формулы расчёта для каждого из этих параметров (m_x, D(x), a_4,a₄) будут зависеть от самой функции распределения f(x) и, следовательно, для различных законов распределения они будут различны.

Основные законы распределения непрерывных случайных величин.

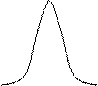
I.  Нормальное распределение Гаусса.

                                                                     f(x)

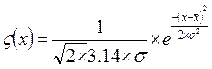
M(x)=m_x, D(x)=s_x, a₃=0_, a₄=0

m_{x                       X}

Примеры применения:

Погрешности обработки и измерения, вызванные одновременным действием большого числа факторов:

-  погрешности линейных и угловых размеров;

-  погрешности ошибок измерения;

-    погрешности оценок шероховатости, массы деталей, механических свойств материалов и др.

II.  Равномерное (прямоугольное)f(x)

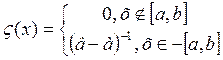                                      (b-a)^-1                       

M(x)=(a+b)/2 ; D(x)= (b-a)^-1/2;  a₃=0; a₄=-1.2                         a            b         x

Примеры применения:

-  ошибка округления при проведении числовых расчётов;

             -    время ожидания обслуживания при точно периодическом включении обслуживающего устройства.

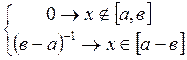
III.       Экспоненциальное (показательное)                      f(x)

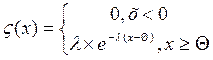                                           l

M(x)=q+l^-1; D(x)=l^-2; a₃=2; a₄=6

q  x

Примеры применения:

Применяется для определения времени безотказной работы при постоянной интенсивности отказов:

           -     время обслуживания специализированным устройствам в некоторых системах массового обслуживания;

-  долговечность издилия, работающего в нормальном режиме эксплуатации.

IV.     Распределение Вейбула-Гнеденко                        f(x)

Частичные случаи распределения:             f(x)    aÎ(0,1)

a=1- экспоненциальное                                                  a>1

a=2- распределение Релея                                                                

                                                                                                  a=1

          0, x £ q

f(x)=    lax^a-1e^-lxa                                                                               x

M(x)=l^-1/av₁; D(x)=l^-1(v₂-v²₁);

Примеры применения:

Долговечность изделия, работающего в режиме приработки (0<a<1),нормальной эксплуатации(a=1) или износа и старения (a>1).   

 Однако на практике ни мат. ожидание, ни генеральную дисперсию по этим формулам не рассчитывают и поступают проще:

Например, для случая нормального распределения вместо мат. ожидания центр распределения оценивают по среднему арифметическому х :

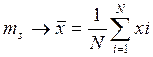
А дисперсию и, соответственно, среднее квадратическое отклонение рассчитывают по формуле:

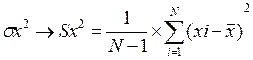
В чем же разница между m_x и x   и соответственно между s_x и S_x?

Чтобы ответить на этот вопрос введем ещё два фундаментальных понятия статической теории: генеральной совокупности и выборки

Генеральная совокупность – это совокупность всех возможных результатов наблюдений над случайной величиной, которые в принципе могут быть проведены при данных условиях. Генеральная совокупность – это теоретическое понятие, т.к. проведение неограничено большого количества испытаний невозможно. Поэтому вынуждены прибегать к ограниченому числу измерений, которое получило название выборки.

Выборка – конечный набор значений случайной величины, полученый в результате наблюдений. Число элементов выборки называют её объёмом и обычно обозначают N. Выборки подразделяются на повторные и безповторные. Повторной называют выборку при которой отобранный объект возвращается в генеральную совокупность, а безповторной – выборку, при которой отобранный объект в генеральную совокупность не возвращается.