Случайной называется величина, значение которой изменяется непредсказуемо при повторении опытов. Поэтому случайную погрешность можно рассматривать как разновидность случайной величины.
Если классифицировать случайные величины, то бывают:
1. Дискретные (пример: число попаданий в цель при определенном количестве выстрелов).
2. Непрерывные (случай, когда число возможных значений случайной величины бесконечно).
Как же можно задать, определить случайную величину, если нельзя заранее точно узнать какое конкретное значение она примет в определенных условиях?
Случайная величина задана, если указан закон ее распределения.
Закон распределения случайной величины - это соответствие между возможными значениями измеряемой величины и их вероятностями.
Основным понятием в этом определении является вероятность.
Вероятность – это числовая характеристика возможности появления некоторого определенного события в цепи событий (которые могут повторяться неограниченное число раз). Приближенной характеристикой вероятности случайного процесса является относительная частота – отношение числа испытаний, в которых событие появилось к общему числу фактических произведенных испытаний. Пример: было произведено 120 выстрелов, из них 102 попадания, следовательно относительная частота поражения цели р(А)= 102/120=0,85
Наблюдения показали, что если в одинаковых условиях проводить опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости.
Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (причем тем меньше, чем больше проведено испытаний), колеблясь около некоторого числа, которое является вероятностью появления этого события.
Иными словами, вероятность события – есть предельное значение частоты его появления при бесконечном числе испытаний.
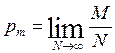
![]()
Некоторые свойства вероятности:
1. Из определения следует, что относительная частота может колебаться от 0 до 1, а следовательно и значение вероятности р(А) некоторого события А находится в тех же пределах.
2. Если Е – достоверное событие, т. е. неизбежно происходящее при каждом испытании, то его вероятность р(Е)=1; если В – невозможное событие, т. е. событие, которое заведомо не произойдет ни при одном испытании, то р(В)=0.
3. События называются несовместимыми (попарно несовместимыми), если никакие два из них не могут произойти совместно в одном и том же испытании. Вероятность появления какого-либо одного (безразлично которого) из нескольких событий равна сумме вероятностей этих событий. Это свойство называется законом сложения вероятностей.
Пример: в ящике 5 черных, 3 красных и 2 белых шара. Вероятность вынуть наугад черный шар – 0,5; красный – 0,3; белый – 0,2. Вероятность вынуть любой красный или черный равна: 0,5+0,3=0,8
4. Вероятность появления нескольких несовместных событий равно произведению их вероятностей. Пример: вероятность того, что будут вынуты последовательно черный и красный шары равна 0,5*0,3=0,15 - если первый вынутый шар черный кладется назад, а если он возвращается, то 0,5*3/9=0,5*0,33=0,165.
Способы задания закона распределения:
1. Табличный. В таблицу заносятся сами значения и их вероятности или относительные частоты.
2. Графический:
2.1. в виде гистограммы.
При построении гистограммы в прямоугольных n
координатах по оси абсцисс – откладывают
границы интервалов, а по оси ординат –
соответствующие абсолютные или
относительные частоты. На гистограмме
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() каждая группа изображается прямоугольником,
каждая группа изображается прямоугольником,
ширина которого пропорциональна ширине x
группы, а высота – частоте. Площадь
отдельных прямоугольников прямопропорциональна групповой частоте, а площадь всех прямоугольников – общему числу наблюдений.
2.2. в виде полигона.
n Полигон получается,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.